
【题目】如图是一个几何体的平面展开图,其中四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,
,![]() ,
,![]() 为全等的等边三角形,
为全等的等边三角形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,在此几何体中,下列结论中正确的个数有()
的中点,在此几何体中,下列结论中正确的个数有()
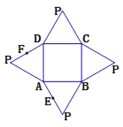
①平面![]() 平面
平面![]()
②直线![]() 与直线
与直线![]() 是异面直线
是异面直线
③直线![]() 与直线
与直线![]() 共面
共面
④面![]() 与面
与面![]() 的交线与
的交线与![]() 平行
平行
A. 3B. 2C. 1D. 0
【答案】A
【解析】
根据展开图,复原几何体,利用异面直线的定义可以判断出②③的正误,利用面面垂直的判定定理判断①的正误,利用面面平行的性质定理判断④的正误,最后选出正确答案.
根据展开图,复原几何体,如下图所示:

由已知条件,在平面![]() 内,过点
内,过点![]() 的中线垂直于
的中线垂直于![]() ,再也找不到和平面
,再也找不到和平面![]() 内垂直的线段,因此找不到和平面
内垂直的线段,因此找不到和平面![]() 垂直的垂线,由已知四边形
垂直的垂线,由已知四边形![]() 为正方形,能得到
为正方形,能得到![]() 或
或![]() ,再也找不到和平面
,再也找不到和平面![]() 内相垂直的的线段,因此找不到和平面
内相垂直的的线段,因此找不到和平面![]() 垂直的线段,所以不能判断平面
垂直的线段,所以不能判断平面![]() 平面
平面![]() ,故①是不正确的;
,故①是不正确的;
根据异面直线的定义可以判断②是正确的;
因为![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,所以
的中点,所以![]() ,而四边形
,而四边形![]() 为正方形,所以有
为正方形,所以有![]() ,因此有
,因此有![]() ,所以
,所以![]() 中点共面,所以③是正确的;
中点共面,所以③是正确的;
因为![]() ,
,![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以面
,所以面![]() 与面
与面![]() 的交线与
的交线与![]() 平行,故④正确,故有三个结论是正确的,本题选A.
平行,故④正确,故有三个结论是正确的,本题选A.


科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,网络搜题软件走进了生活,有教育工作者认为,网搜答案可以起到帮助人们学习的作用,但对多数学生来讲,过度网搜答案容易养成依赖心理,对学习能力造成损害.为了了解学生网搜答案的情况,某学校对学生一月内进行网搜答案的次数进行了问卷调查,并从参与调查的学生中抽取了男、女生各100人进行抽样分析,制成如下频率分布直方图:

记事件“男生1月内网搜答案次数不高于30次”为![]() ,根据频率分布直方图得到
,根据频率分布直方图得到![]() 的估计值为0.65
的估计值为0.65
(1)求![]() 的值;
的值;
(2)若一学生在1月内网搜答案次数超过50次,则称该学生为“依赖型”,现从样本内的“依赖型”学生中,抽取3人谈话,求抽取的女生人数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)的定义域为(0,+∞),且满足f(2)=1,f(xy)=f(x)+f(y),又当x2>x1>0时,f(x2)>f(x1).
(1)求f(1)、f(4)、f(8)的值;
(2)若有f(x)+f(x-2)≤3成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理财公司有两种理财产品A和B,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品A
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概率 |
|
|
|
产品B
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概率 | p |
| q |
注:p>0,q>0
(1)已知甲、乙两人分别选择了产品A和产品B投资,如果一年后他们中至少有一人获利的概率大于![]() ,求实数p的取值范围;
,求实数p的取值范围;
(2)若丙要将家中闲置的10万元人民币进行投资,以一年后投资收益的期望值为决策依据,则选用哪种产品投资较理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一般认为,民用住宅的窗户面积必须小于地板面积,但窗户面积与地板面积的比应不小于10%,而且这个比值越大,采光效果越好.
(1)若一所公寓窗户面积与地板面积的总和为![]() ,则这所公寓的窗户面积至少为多少平方米?
,则这所公寓的窗户面积至少为多少平方米?
(2)若同时增加相同的窗户面积和地板面积,公寓的采光效果是变好了还是变坏了?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为![]() 的圆过原点
的圆过原点![]() ,且直线
,且直线![]() 与圆
与圆![]() 相切于点
相切于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)已知过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点.
两点.
①若![]() ,求弦
,求弦![]() 的长;
的长;
②若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() 成立,求直线
成立,求直线![]() 的斜率
的斜率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】火车站有某公司待运的甲种货物![]() ,乙种货物
,乙种货物![]() ,现计划用A,B两种型号的货厢共50节运送这批货物,已知35t甲种货物和15
,现计划用A,B两种型号的货厢共50节运送这批货物,已知35t甲种货物和15![]() 乙种货物可装满一节A型货厢,25t甲种货物和35
乙种货物可装满一节A型货厢,25t甲种货物和35![]() 乙种货物可装满一节B型货厢,据此安排A,B两种货厢的节数,共有几种方案?若每节A型货厢的运费是0.5万元,每节B型货用的运费是0.8万元,哪种方案的运费较少?
乙种货物可装满一节B型货厢,据此安排A,B两种货厢的节数,共有几种方案?若每节A型货厢的运费是0.5万元,每节B型货用的运费是0.8万元,哪种方案的运费较少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知某区甲、乙、丙三所学校的教师志愿者人数分别为240,160,80.为助力疫情防控,现采用分层抽样的方法,从这三所学校的教师志愿者中抽取6名教师,参与“抗击疫情·你我同行”下卡口执勤值守专项行动.
(Ⅰ)求应从甲、乙、丙三所学校的教师志愿者中分别抽取的人数;
(Ⅱ)设抽出的6名教师志愿者分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,现从中随机抽取2名教师志愿者承担测试体温工作.
,现从中随机抽取2名教师志愿者承担测试体温工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2名教师志愿者来自同一所学校”,求事件
为事件“抽取的2名教师志愿者来自同一所学校”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛掷一个质地均匀的骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“不小于5的点数出现”,则一次试验中,事件A或事件B至少有一个发生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com