
 如图已知平行六面体ABCD-A′B′C′D′,E、F、G、H分别是棱A′D′、D′C′、C′C和AB的中点,求证E、F、G、H四点共面.
如图已知平行六面体ABCD-A′B′C′D′,E、F、G、H分别是棱A′D′、D′C′、C′C和AB的中点,求证E、F、G、H四点共面.| ED′ |
| a |
| EF |
| b |
| EH |
| c |
| HG |
| HB |
| BC |
| CG |
| D′F |
| ED′ |
| 1 |
| 2 |
| AA′ |
| HG |
| 3 |
| 2 |
| b |
| 1 |
| 2 |
| c |
| HG |
| EF |
| EH |
| ED′ |
| a |
| EF |
| b |
| EH |
| c |

| HB |
| D′F |
| b |
| a |
| BC |
| ED′ |
| a |
| CG |
| 1 |
| 2 |
| AA′ |
| HG |
| HB |
| BC |
| CG |
| D′F |
| ED′ |
| 1 |
| 2 |
| AA′ |
| b |
| a |
| a |
| 1 |
| 2 |
| AH |
| HE |
| EA′ |
| b |
| a |
| 1 |
| 2 |
| b |
| a |
| c |
| a |
| 3 |
| 2 |
| b |
| 1 |
| 2 |
| c |
| HG |
| b |
| c |
| HG |
| EF |
| EH |


科目:高中数学 来源: 题型:
 已知平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,
已知平行六面体ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,| AC/ |
| AC |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且| OA |
| a |
| OC |
| b |
| OO1 |
| c |
| a |
| b |
| c |
| OG |
查看答案和解析>>
科目:高中数学 来源: 题型:
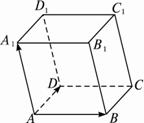
 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.| A1M |
| MG |
| AB |
| AD |
| AA1 |
| A1M |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)|![]() |;?
|;?
(2)〈![]() ,
,![]() 〉的大小(用a、b表示).?
〉的大小(用a、b表示).?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com