
【题目】已知f(x)是定义在R上的奇函数,当x>0时,f(x)= ![]() x3+ax(a∈R),且曲线f(x)在x=
x3+ax(a∈R),且曲线f(x)在x= ![]() 处的切线与直线y=﹣
处的切线与直线y=﹣ ![]() x﹣1平行.
x﹣1平行.
(Ⅰ)求a的值及函数f(x)的解析式;
(Ⅱ)若函数y=f(x)﹣m在区间[﹣3, ![]() ]上有三个零点,求实数m的取值范围.
]上有三个零点,求实数m的取值范围.
【答案】解:(Ⅰ)当x>0时,f′(x)=x2+a, 因为曲线f(x)在x= ![]() 处的切线与直线y=﹣
处的切线与直线y=﹣ ![]() x﹣1平行,
x﹣1平行,
所以f′( ![]() )=
)= ![]() +a=﹣
+a=﹣ ![]() ,解得a=﹣1,
,解得a=﹣1,
所以f(x)= ![]() x3﹣x,
x3﹣x,
设x<0则f(x)=﹣f(﹣x)= ![]() x3﹣x,
x3﹣x,
又f(0)=0,所以f(x)= ![]() x3﹣x.
x3﹣x.
(Ⅱ)由(Ⅰ)知f(﹣3)=﹣6,f(﹣1)= ![]() ,f(1)=﹣
,f(1)=﹣ ![]() ,f(
,f( ![]() )=0,
)=0,
所以函数y=f(x)﹣m在区间[﹣3, ![]() ]上有三个零点,
]上有三个零点,
等价于函数f(x)在[﹣3, ![]() ]上的图象与y=m有三个公共点.
]上的图象与y=m有三个公共点.
结合函数f(x)在区间[﹣3, ![]() ]上大致图象可知,实数m的取值范围是(﹣
]上大致图象可知,实数m的取值范围是(﹣ ![]() ,0).
,0).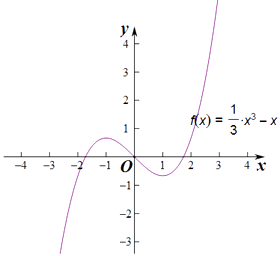
【解析】(Ⅰ)首先求得导函数,然后利用导数的几何意义结合两直线平行的关系求得a的值,由此求得函数f(x)的解析式;(Ⅱ)将问题转化为函数f(x)的图象与y=m有三个公共点,由此结合图象求得m的取值范围.
【考点精析】解答此题的关键在于理解基本求导法则的相关知识,掌握若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.


科目:高中数学 来源: 题型:
【题目】阅读下面材料,完成数学问题.
我校高二文科班的同学到武昌农民运动讲习所研学的途中路过武汉长江大桥边的武昌长江大堤,同学们在大堤上看到与武昌隔江相对的汉阳龟山上的电视塔和汉阳江边的晴川饭店在朝阳的映照下显得非常美丽,纷纷拿出手机拍照。这时带队的老师问大家,我要站在武昌大堤的哪一点才能够同时拍下电视塔和晴川饭店最清晰的图像?听到这个问题后,同学们议论纷纷。讨论一会后,一个同学对大家说:“把电视塔看成点A,饭店看成点B,武昌大堤看成直线l,C是直线l上的动点,拍照最佳点就是直线上使∠ACB最大的点.使∠ACB最大的点的求法用初中数学的一个定理:过点A,B作与直线l相切的圆,半径较小的圆和直线l的切点就是直线l上使∠ACB最大的点。”老师和同学们听了拍手称对。回到学校后,一位同学利用百度地图测距功能测得点A到直线l距离是2km,点B到直线l距离是1.5km,A,B两点间的距离是1km.该同学以直线l为x轴,过A点和直线l垂直的直线为y轴建立了如图所示的坐标系,点A的坐标为(0, 2),点B在第一象限.根据以上材料,请在所给的坐标系中,在x轴上求使∠ACB最大的点的坐标.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin2x+ ![]() cos2x图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有点向右平移
cos2x图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有点向右平移 ![]() 个单位长度,得到函数g (x)的图象,则g(x)图象的一条对称轴方程是( )
个单位长度,得到函数g (x)的图象,则g(x)图象的一条对称轴方程是( )
A.x=一 ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD= ![]() ,则直线AD与平面BCD所成角的大小是( )
,则直线AD与平面BCD所成角的大小是( ) 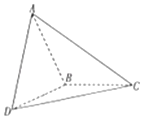
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,2acosC=bcosC+ccosB.
(1)求角C的大小;
(2)若c=![]() ,a2+b2=10,求△ABC的面积.
,a2+b2=10,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,4),且斜率为![]() 的直线与圆C:
的直线与圆C:![]() ,相交于不同两点M、N.
,相交于不同两点M、N.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证:![]() 为定值;
为定值;
(3)若O为坐标原点,问是否存在以MN为直径的圆恰过点O,若存在则求![]() 的值,若不存在,说明理由。
的值,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数),直线l的参数方程为
(α为参数),直线l的参数方程为  (t为参数),在以坐标原点O为极点,x轴为正半轴为极轴的极坐标系中,过极点O的射线与曲线C相交于不同于极点的点A,且点A的极坐标为(2
(t为参数),在以坐标原点O为极点,x轴为正半轴为极轴的极坐标系中,过极点O的射线与曲线C相交于不同于极点的点A,且点A的极坐标为(2 ![]() ,θ),其中θ∈(
,θ),其中θ∈( ![]() ,π)
,π)
(Ⅰ)求θ的值;
(Ⅱ)若射线OA与直线l相交于点B,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
设函数f(x)=|x﹣1|﹣|2x+1|的最大值为m.
(1)作出函数f(x)的图象;
(2)若a2+2c2+3b2=m,求ab+2bc的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com