[题目]已知椭圆上的点到两个焦点的距离之和为.短轴长为.直线与椭圆交于.两点.(1)求椭圆的方程, (2)若直线与圆相切.探究是否为定值.如果是定值.请求出该定值,如果不是定值.请说明理由．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知椭圆上的点到两个焦点的距离之和为，短轴长为，直线与椭圆交于、两点.

（1）求椭圆的方程；

（2）若直线与圆相切，探究是否为定值，如果是定值，请求出该定值；如果不是定值，请说明理由．

【答案】（1）（2）

【解析】试题分析：（1）由已知得由此能求出椭圆的方程．
（2）当直线轴时，．当直线与轴不垂直时，设直线直线与与圆的交点M（x1，y1），N（x2，y2），由直线与圆相切，得，联立，得（，由此能证明为定值．

试题解析：

1）由题意得

（2）当直线轴时，因为直线与圆相切，所以直线方程为

当时，得M、N两点坐标分别为，

当时，同理；

当与轴不垂直时，

设，由,

联立得

，， =

综上，（定值）

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在下列向量组中，可以把向量 =（3，2）表示出来的是（）
A. =（0，0）， =（1，2）
B. =（﹣1，2）， =（5，﹣2）
C. =（3，5）， =（6，10）
D. =（2，﹣3）， =（﹣2，3）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某金匠以黄金为原材料加工一种饰品，经多年的数据统计得知，该金匠平均每加5 个饰品中有4个成品和1个废品，每个成品可获利3万元，每个废品损失1万元，假设该金匠加工每件饰品互不影响，以频率估计概率.

（1）若金金匠加工4个饰品，求其中废品的数量不超过1的概率；

（2）若该金匠加工了 3个饰品，求他所获利润的数学期望.

(两小问的计算结果都用分数表示）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在△ABC中，角A，B，C的对边分别为a，b，c， asinB+bcosA=c．（Ⅰ）求B；
（Ⅱ）若a=2 c，S△ABC=2 ，求b．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥中，底面，底面是直角梯形，，，，是上的点．

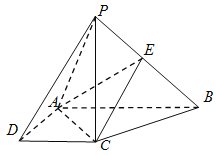
（Ⅰ）求证：平面⊥平面；

（Ⅱ）若是的中点，且二面角的余弦值为，求直线与平面所成角的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】《数学九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白，与著名的海伦公式完全等价，由此可以看出我国古代已具有很高的数学水平，其求法是：“以小斜幂并大斜幂减中斜幂，余半之，自乘于上．以小斜幂乘大斜幂减上，余四约之，为实．一为从隔，开平方得积．”若把以上这段文字写成公式，即S= ．现有周长为2 + 的△ABC满足sinA：sinB：sinC=（ ﹣1）：：（ +1），试用以上给出的公式求得△ABC的面积为（）
A.
B.
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】甲乙丙丁四个物体同时从某一点出发向同一个方向运动，其路程fi（x）（i=1，2，3，4）关于时间x（x≥0）的函数关系式分别为，有以下结论：
①当x＞1时，甲在最前面；
②当x＞1时，乙在最前面；
③当0＜x＜1时，丁在最前面，当x＞1时，丁在最后面；
④丙不可能在最前面，也不可能最最后面；
⑤如果它们已知运动下去，最终在最前面的是甲．
其中，正确结论的序号为（把正确结论的序号都填上，多填或少填均不得分）