【题目】设函数
，其中
，若
、
、
是
的三条边长，则下列结论：①对于一切
都有
；②存在
使
、
、
不能构成一个三角形的三边长；③为钝角三角形，存在
，使
，其中正确的个数为______个
A. 3B. 2C. 1D. 0
激活思维优加课堂系列答案
活力试卷系列答案科目：高中数学 来源： 题型：
【题目】交通指数是指交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念性指数值，记交通指数为
，其范围为
，分别有五个级别：
，畅通；
，基本畅通；
，轻度拥堵；
，中度拥堵；
，严重拥堵.在晚高峰时段（
），从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制的频率分布直方图如图所示.
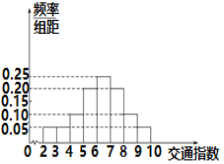
(1)求出轻度拥堵、中度拥堵、严重拥堵的路段的个数；
(2)用分层抽样的方法从轻度拥堵、中度拥堵、严重拥堵的路段中共抽取6个路段，求依次抽取的三个级别路段的个数；
(3)从(2)中抽取的6个路段中任取2个，求至少有1个路段为轻度拥堵的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某污水处理厂要在一个矩形污水处理池
的池底水平铺设污水净化管道（
，
是直角顶点）来处理污水，管道越长，污水净化效果越好．设计要求管道的接口是
的中点，
分别落在线段
上．已知
米，
米，记
．
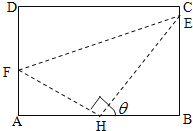
（1）试将污水净化管道的长度
表示为
的函数，并写出定义域；
（2）若
，求此时管道的长度；
（3）当取何值时，污水净化效果最好？并求出此时管道的长度．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙、丙
人投篮，投进的概率分别是
，
，
.
（1）现人各投篮
次，求人至少一人投进的概率；
（2）用
表示乙投篮
次的进球数，求随机变量的概率分布及数学期望
和方差
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】学校计划在全国中学生田径比赛期间，安排6位志愿者到4个比赛场地提供服务，要求甲、乙两个比赛场地各安排一个人，剩下两个比赛场地各安排两个人，其中的小李和小王不在一起，不同的安排方案共有( )
A. 168种 B. 156种 C. 172种 D. 180种
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地区100位居民的人均月用水量(单位：
)的分组及各组的频数如下：
，4； 
，8； 
，15；
，22； 
，25； 
，14；
，6； 
，4； 
，2．
(1)列出样本的频率分布表；
(2)画出频率分布直方图，并根据直方图估计这组数据的平均数、中位数、众数；
(3)当地政府制定了人均月用水量为
的标准，若超出标准加倍收费，当地政府说，
以上的居民不超过这个标准，这个解释对吗？为什么？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了研究高中学生对乡村音乐的态度（喜欢和不喜欢两种态度）与性别的关系，运用2×2列联表进行独立性检验，经计算K2=8.01，附表如下：
P（K2≥k0） | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参照附表，得到的正确的结论是（ ）
A. 有99%以上的把握认为“喜欢乡村音乐与性别有关”
B. 有99%以上的把握认为“喜欢乡村音乐与性别无关”
C. 在犯错误的概率不超过0.1%的前提下，认为“喜欢乡村音乐与性别有关”
D. 在犯错误的概率不超过0.1%的前提下，认为“喜欢乡村音乐与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
