
【题目】某医院对治疗支气管肺炎的两种方案![]() ,
,![]() 进行比较研究,将志愿者分为两组,分别采用方案
进行比较研究,将志愿者分为两组,分别采用方案![]() 和方案
和方案![]() 进行治疗,统计结果如下:
进行治疗,统计结果如下:
有效 | 无效 | 合计 | |
使用方案 | 96 | 120 | |
使用方案 | 72 | ||
合计 | 32 |
(1)完成上述列联表,并比较两种治疗方案有效的频率;
(2)能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关?
附: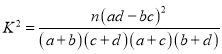 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若a=0时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)若函数![]() 在x=1时取极大值,求实数a的取值范围;
在x=1时取极大值,求实数a的取值范围;
(3)设函数![]() 的零点个数为m,试求m的最大值.
的零点个数为m,试求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B两地相距100公里,两地政府为提升城市的抗疫能力,决定在A、B之间选址P点建造储备仓库,共享民生物资,当点P在线段AB的中点C时,建造费用为2000万元,若点P在线段AC上(不含点A),则建造费用与P、A之间的距离成反比,若点P在线段CB上(不含点B),则建造费用与P、B之间的距离成反比,现假设P、A之间的距离为x千米![]() ,A地所需该物资每年的运输费用为
,A地所需该物资每年的运输费用为![]() 万元,B地所需该物资每年的运输费用为
万元,B地所需该物资每年的运输费用为![]() 万元,
万元,![]() 表示建造仓库费用,
表示建造仓库费用,![]() 表示两地物资每年的运输总费用(单位:万元).
表示两地物资每年的运输总费用(单位:万元).
![]()
(1)求函数![]() 的解析式;
的解析式;
(2)若规划仓库使用的年限为![]() ,
,![]() ,求
,求![]() 的最小值,并解释其实际意义.
的最小值,并解释其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在数列![]() 的一个无穷子数列
的一个无穷子数列![]() ,使
,使![]() 对一切
对一切![]() 均成立?若存在,请写出数列
均成立?若存在,请写出数列![]() 的所有通项公式;若不存在,请说明理由.
的所有通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,需引进一条新的生产线投入生产,现有两条生产线可供选择,生产线①:有A,B两道独立运行的生产工序,且两道工序出现故障的概率依次是0.02,0.03.若两道工序都没有出现故障,则生产成本为15万元;若A工序出现故障,则生产成本增加2万元;若B工序出现故障,则生产成本增加3万元;若A,B两道工序都出现故障,则生产成本增加5万元.生产线②:有a,b两道独立运行的生产工序,且两道工序出现故障的概率依次是0.04,0.01.若两道工序都没有出现故障,则生产成本为14万元;若a工序出现故障,则生产成本增加8万元;若b工序出现故障,则生产成本增加5万元;若a,b两道工序都出现故障,则生产成本增加13万元.
(1)若选择生产线①,求生产成本恰好为18万元的概率;
(2)为最大限度节约生产成本,你会给工厂建议选择哪条生产线?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知曲线
中,已知曲线![]() :
: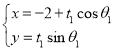 (
(![]() 为参数),曲线
为参数),曲线![]() :
: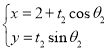 (
(![]() 为参数),且
为参数),且![]() ,点P为曲线
,点P为曲线![]() 与
与![]() 的公共点.
的公共点.
(1)求动点P的轨迹方程;
(2)在以原点O为极点,x轴的非负半轴为极轴的极坐标系中,直线l的极坐标方程为![]() ,求动点P到直线l的距离的取值范围.
,求动点P到直线l的距离的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com