
【题目】乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求乙以4比1获胜的概率;
(2)求甲获胜且比赛局数多于5局的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)记“乙以4比1获胜”为事件A ,,则A表示乙赢了3局甲赢了1局,且第五局乙赢,再根据n次独立重复实验中恰好发生k次的概率计算公式求得![]() 的值。(2)利用n次独立重复实验中恰好发生k次的概率计算公式求得甲以4比2获胜的概率,以及甲以4比3获胜的概率,再把这2个概率值相加,即得所求。
的值。(2)利用n次独立重复实验中恰好发生k次的概率计算公式求得甲以4比2获胜的概率,以及甲以4比3获胜的概率,再把这2个概率值相加,即得所求。
解:(1)由已知,甲、乙两名运动员在每一局比赛中获胜的概率都是![]() ,
,
记“乙以4比1获胜”为事件A,则A表示乙赢了3局甲赢了一局,且第五局乙赢,
∴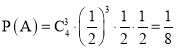 .
.
(2)记“甲获胜且比赛局数多于5局”为事件B,则B表示甲以4比2获胜,或甲以4比3获胜.
因为甲以4比2获胜,表示前5局比赛中甲赢了3局且第六局比赛中甲赢了,
这时,无需进行第7局比赛,故甲以4比2获胜的概率为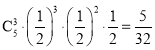 .
.
甲以4比3获胜,表示前6局比赛中甲赢了3局且第7局比赛中甲赢了,
故甲以4比3获胜的概率为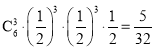 ,
,
故甲获胜且比赛局数多于5局的概率为![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的横坐标变为原来的2倍,纵坐标变为原来的4倍,得曲线
上每一点的横坐标变为原来的2倍,纵坐标变为原来的4倍,得曲线![]() .
.
(1)写出![]() 的参数方程;
的参数方程;
(2)设直线![]() 与
与![]() 的交点为
的交点为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,求过线段
轴正半轴为极轴建立极坐标系,求过线段![]() 的中点与
的中点与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|lnx|,若函数g(x)=f(x)-ax在区间(0,4)上有三个零点,则实数a的取值范围是( )
A. (0,![]() )B. (
)B. (![]() ,e)C. (
,e)C. (![]() ,
,![]() )D. (0,
)D. (0,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”; ③“
”; ③“![]() ,则
,则![]() ”的否定是“
”的否定是“![]() ,则
,则![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题的个数是( )
”的充要条件.其中正确的命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,如果存在区间
,如果存在区间![]() ,同时满足:①函数在区间内是单调函数;②当定义域为
,同时满足:①函数在区间内是单调函数;②当定义域为![]() 时,
时,![]() 的值域也是
的值域也是![]() ,则称
,则称![]() 是该函数的和谐区间.
是该函数的和谐区间.
(1)求证:函数![]() 不存在和谐区间;
不存在和谐区间;
(2)已知:函数![]() 有和谐区间
有和谐区间![]() ,当
,当![]() 变化时,求出
变化时,求出![]() 的最大值;
的最大值;
(3)易知,函数![]() 是以任一区间为它的“和谐区间”,试再举一例有和谐区间的函数,并写出它的个和谐区间(不需要证明,但是不能用本题已经讨论过的
是以任一区间为它的“和谐区间”,试再举一例有和谐区间的函数,并写出它的个和谐区间(不需要证明,但是不能用本题已经讨论过的![]() 以及形如
以及形如![]() 的函数).
的函数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接中国共产党的十九大的到来,某校举办了“祖国,你好”的诗歌朗诵比赛.该校高三年级准备从包括甲、乙、丙在内的7名学生中选派4名学生参加,要求甲、乙、丙这3名同学中至少有1人参加,且当这3名同学都参加时,甲和乙的朗诵顺序不能相邻,那么选派的4名学生不同的朗诵顺序的种数为( )
A. 720 B. 768 C. 810 D. 816
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com