
分析 (1)f(x)解析式利用二倍角正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,找出ω的值,代入周期公式求出最小正周期,由正弦函数的单调性确定出f(x)的单调递减区间即可;
(2)由f(x)解析式,以及f($\frac{A}{2}$-$\frac{π}{6}$)=$\sqrt{3}$,求出A的度数,将sinB+sinC=$\frac{13\sqrt{3}}{14}$,利用正弦定理化简,求出bc的值即可.
解答 解:(1)f(x)=2sinx•cosx+2$\sqrt{3}$cos2x-$\sqrt{3}$=sin2x+$\sqrt{3}$cos2x=2sin(2x+$\frac{π}{3}$),
∵ω=2,∴f(x)的最小正周期T=π,
∵2kπ+$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈Z,
∴f(x)的单调减区间为[kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$],k∈Z;
(2)由f($\frac{A}{2}$-$\frac{π}{6}$)=2sin[2($\frac{A}{2}$-$\frac{π}{6}$)+$\frac{π}{3}$]=2sinA=$\sqrt{3}$,即sinA=$\frac{\sqrt{3}}{2}$,
∵A为锐角,∴A=$\frac{π}{3}$,
由正弦定理可得2R=$\frac{a}{sinA}$=$\frac{7}{\frac{\sqrt{3}}{2}}$=$\frac{14\sqrt{3}}{3}$,sinB+sinC=$\frac{b+c}{2R}$=$\frac{13\sqrt{3}}{14}$,
∴b+c=$\frac{13\sqrt{3}}{14}$×$\frac{14}{\sqrt{3}}$=13,
由余弦定理可知:cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{(b+c)^{2}-2bc-{a}^{2}}{2bc}$=$\frac{1}{2}$,
整理得:bc=40.
点评 此题考查了正弦、余弦定理,以及三角函数中的恒等变换应用,熟练掌握定理是解本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
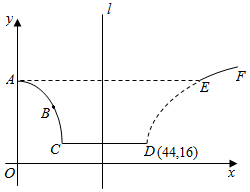 在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xOy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老张预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.现在老张决定取点A(0,22),点B(12,19),点D(44,16)来确定解析式中的常数a,b,ω,φ,并且求得ω=$\frac{π}{72}$
在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xOy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老张预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.现在老张决定取点A(0,22),点B(12,19),点D(44,16)来确定解析式中的常数a,b,ω,φ,并且求得ω=$\frac{π}{72}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x<log2x<${({\frac{1}{2}})^x}$ | B. | 2x<${({\frac{1}{2}})^x}$<log2x | C. | ${({\frac{1}{2}})^x}$<log2x<2x | D. | log2x<${({\frac{1}{2}})^x}$<2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,4] | B. | [2,3] | C. | [-2,4] | D. | [-2,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com