
分析 (1)利用和差角(辅助角)公式,可得f(x)=cosωx,将点A($\frac{π}{4}$,0)代入结合0<ω<3,可得ω的值,进而得到函数的周期;
(2)利用和差角(辅助角)公式,可得g(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),结合α∈(0,π),且g($\frac{α}{2}$)=0,可得α的值.
解答 解:(1)∵函数f(x)=$\frac{1}{2}$sin(ωx+$\frac{π}{6}$)+$\frac{\sqrt{3}}{2}cos(ωx+\frac{π}{6})$=sin(ωx+$\frac{π}{6}$+$\frac{π}{3}$)=sin(ωx+$\frac{π}{2}$)=cosωx的图象过点A($\frac{π}{4}$,0).
∴cos$\frac{ωπ}{4}$=0,
又∵0<ω<3,
∴ω=2,
∴T=$\frac{2π}{2}$=π;
(2)由(1)得:函数f(x)=cos2x,
∴g(x)=f(x)+sin2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
若($\frac{α}{2}$)=0,
则sin(α+$\frac{π}{4}$)=0,
又∵α∈(0,π),
∴$α=\frac{3π}{4}$.
点评 本题考查的知识点是正弦型函数的图象和性质,二倍角公式和和差角(辅助角)公式,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左或向右平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向左或向右平移$\frac{3π}{2}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{3}{11}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ①② | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
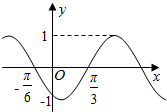
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆N:(x+1)2+y2=2的切线l与抛物线C:y2=x交于不同的两点A,B.
已知圆N:(x+1)2+y2=2的切线l与抛物线C:y2=x交于不同的两点A,B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com