练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图3-3-3，在直角坐标系内，射线OT落在60°角的终边上，任作一条射线OA，求射线OA落在∠xOT内的概率.

           图3-3-3

    解：以O为起点作射线OA是随机的，因而射线OA落在任何位置都是等可能的.

    落在∠xOT内的概率只与∠xOT的大小有关，符合几何概型的条件.

    记事件B=｛射线OA落在∠xOT内｝.

    因为∠xOT=60°，所以P(B)=.

        巧解提示 本例中“成比例”的量，既不是长度，也不是面积和体积，而是角度，这与教材中几何概型的定义不相符.但因为一是教材中有关几何概型的定义不是严格的定义；二是教材中的定义只是说明了当随机事件与其基本事件具备这种“成比例”的条件时，我们便可以利用“成比例”求其概率的思想方法,所以在本例中，我们可以利用“角度”成比例来求其概率.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

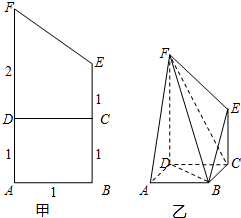    将（如图甲）直角梯形ABEF（图中数字表示对应线段的长度）沿直线CD折成直二面角，连接部分线段后围成一个空间几何体，如图乙所示．
    （1）求异面直线BD与EF所成角的大小；
    （2）求二面角D-BF-E的大小．
    （3）若F、A、B、C、D这五个点在同一个球面上，求该球的表面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一青蛙从点A0（x0，y0）开始依次水平向右和竖直向上跳动，其落点坐标依次是Ai（xi，yi）（i∈N*），（如图所示，A0（x0，y0）坐标以已知条件为准），Sn表示青蛙从点A0到点An所经过的路程．
    （1）若点A0（x0，y0）为抛物线y2=2px（p＞0）准线上一点，点A1，A2均在该抛物线上，并且直线A1A2经过该抛物线的焦点，证明S2=3p．
    （2）若点An（xn，yn）要么落在y=x所表示的曲线上，要么落在y=x2所表示的曲线上，并且A0(
    1
    2
    ，
    1
    2
    )    ，试写出
    lim
    n→+∞
    Sn    （不需证明）；
    （3）若点An（xn，yn）要么落在y=2
    		1+8x
    -1    所表示的曲线上，要么落在y=2
    		1+8x
    +1    所表示的曲线上，并且A0（0，4），求Sn的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    如图3-3，某市现有自市中心O通往正西和东北方向的两条主要公路，为了解决市交通拥挤问题，市政府决定修建一条环城公路．分别在通往正西和东北方向的公路上选取A、B两点，使环城公路在A、B间为直线段，要求AB路段与市中心O的距离为10km，且使A、B间的距离|AB|最小．请你确定A、B两点的最佳位置(不要求作近似计算)．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    如图3-3，某市现有自市中心O通往正西和东北方向的两条主要公路，为了解决市交通拥挤问题，市政府决定修建一条环城公路．分别在通往正西和东北方向的公路上选取A、B两点，使环城公路在A、B间为直线段，要求AB路段与市中心O的距离为10km，且使A、B间的距离|AB|最小．请你确定A、B两点的最佳位置(不要求作近似计算)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图3所示，在直三棱柱中，，，，．

    （Ⅰ）证明：平面；

    （Ⅱ）若是棱的中点，在棱上是否存在一点，使平面？证明你的结论．

    查看答案和解析>>

    同步练习册答案