
| A. | $\frac{x^2}{5}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{5}+\frac{y^2}{2}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{10}+\frac{y^2}{16}=1$ |
分析 由题意设出椭圆方程,P的坐标,结合P在椭圆上,可得关于P的横坐标的方程,由判别式大于等于0求得a的范围,进一步求出a的最小值,结合隐含条件求得b,则椭圆方程可求.
解答 解:由题意可设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$( a>b>0),
则c=1,∴a2-b2=c2=1,
设P﹙m.m+3﹚,由P在椭圆上,得$\frac{{m}^{2}}{{a}^{2}}+\frac{(m+3)^{2}}{{a}^{2}-1}=1$,
∴﹙a2-1﹚m2+a2﹙m2+6m+9﹚=a2﹙a2-1﹚=﹙a2﹚2-a2,
即﹙2a2-1﹚m2+6a2m+10a2-﹙a2﹚2=0.
由△=﹙6a2﹚2-﹙8a2-4﹚﹙10a2-a4﹚≥0,
得36a4-80a4++40a2+8a6-4a4≥0,
∴-48a2+40+8a4≥0,a4-6a2+5≥0,
即﹙a2-5﹚﹙a2-1﹚≥0,
解得a2≤1或 a2≥5,
∵c2=1,a2>c2,
∴a2≥5,长轴最短,即a2=5,
则b2=a2-1=4.
∴所求椭圆方程为:$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1$.
故选:A.
点评 本题考查椭圆的简单性质,考查了数学转化思想方法,是中档题.


 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+4x+6≥0 | B. | $?x∈R,{x_0}^2+4{x_0}+6>0$ | ||
| C. | ?x∈R,x2+4x+6>0 | D. | $?x∈R,{x_0}^2+4{x_0}+6≥0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
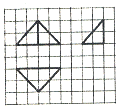
| A. | 8+4$\sqrt{3}$ | B. | 8+4$\sqrt{2}$ | C. | 8+16$\sqrt{2}$ | D. | 8+8$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | ±1 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{3}{4},\frac{3}{4}})$ | B. | $({-\frac{4}{3},\frac{4}{3}})$ | C. | $({0,\frac{3}{4}})$ | D. | $({-\frac{3}{4},0})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组序 | 高度区间 | 频数 | 频率 |
| 1 | [230,235) | 14 | 0.14 |
| 2 | [235,240) | ① | 0.26 |
| 3 | [240,245) | ② | 0.20 |
| 4 | [245,250) | 30 | ③ |
| 5 | [250,255) | 10 | ④ |
| 合计 | 100 | 1.00 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com