
【题目】设函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数)。
为自然对数的底数)。
(Ⅰ)若![]() 在区间
在区间![]() 上存在极值,求实数
上存在极值,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)求证:当![]() 时,不等式
时,不等式![]() 。
。
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析;
;(Ⅱ)证明见解析;
【解析】试题分析:(1)首先利用切线的斜率建立方程,求出![]() ;利用导数求得函数的极值点,极值点介于
;利用导数求得函数的极值点,极值点介于![]() 之间,由此求得
之间,由此求得![]() 的取值范围;(2)先用分析法,将原不等式等价变形为
的取值范围;(2)先用分析法,将原不等式等价变形为![]() ,利用导数求出左边函数的最小值和右边函数的最大值即可证得原不等式成立.
,利用导数求出左边函数的最小值和右边函数的最大值即可证得原不等式成立.
试题解析:
(1) 因为![]() ,所以
,所以![]()
又据题意,得![]() ,所以
,所以![]() ,所以
,所以![]()
所以![]() ,
,
所以![]()
![]()
当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,
,![]() 为减函数.
为减函数.
所以函数![]() 仅当
仅当![]() 时,取得极值
时,取得极值
又函数![]() 在区间
在区间![]() 上存在极值,所以
上存在极值,所以![]() ,所以
,所以![]() .
.
故实数![]() 的取值范围是
的取值范围是![]()
(2)当![]() 时,
时,![]() ,即为
,即为![]() .
.
令![]() ,则
,则![]() .
.
再令![]() ,则
,则![]() .
.
又因为![]() ,所以
,所以![]() .
.
所以![]() 在
在![]() 上是增函数.
上是增函数.
又因为![]() .
.
所以当![]() 时,
时,![]() .
.
所以![]() 在区间
在区间![]() 上是增函数.
上是增函数.
所以当![]() 时,
时,![]() ,又
,又![]() ,故
,故![]()
令![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() .
.
所以当![]() 时,
时,![]() .故函数
.故函数![]() 在区间
在区间![]() 上是减函数.
上是减函数.
又![]() ,
,
所以当![]() 时,
时,![]() ,
,
所以![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2. 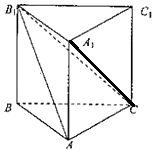
(1)求证:平面B1AC⊥平面ABB1A1;
(2)求直线A1C与平面B1AC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣4ax+b(a>0)在区间[0,1]上有最大值1和最小值﹣2.
(1)求a,b的值;
(2)若不等式f(x)≥mx在x∈(0,+∞)上恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα﹣
=(cosα﹣ ![]() ,﹣1),
,﹣1), ![]() =(sinα,1),
=(sinα,1), ![]() 与
与 ![]() 为共线向量,且α∈[﹣
为共线向量,且α∈[﹣ ![]() ,0].
,0].
(1)求sinα+cosα的值;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若an=log(n+1)(n+2)(n∈N),我们把使乘积a1a2…an为整数的数n叫做“劣数”,则在区间(1,2004)内所有劣数的和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用an的信息如图. 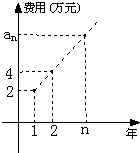
(1)求an;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2. (Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的余弦值.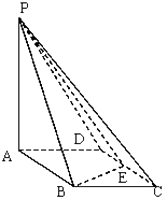
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以边长为![]() 的正三角形
的正三角形![]() 的顶点
的顶点![]() 为坐标原点,另外两个顶点在抛物线
为坐标原点,另外两个顶点在抛物线![]() 上,过抛物线
上,过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 过交拋物线
过交拋物线![]() 于
于![]() 两点.
两点.
(1)求抛物线![]() 的方程;
的方程;
(2)求证: ![]() 为定值;
为定值;
(3)求线段![]() 的中点的轨迹方程.
的中点的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com