
【题目】已知动点P是△PMN的顶点,M(﹣2,0),N(2,0),直线PM,PN的斜率之积为﹣![]() .
.
(1)求点P的轨迹E的方程;
(2)设四边形ABCD的顶点都在曲线E上,且AB∥CD,直线AB,CD分别过点(﹣1,0),(1,0),求四边形ABCD的面积为![]() 时,直线AB的方程.
时,直线AB的方程.
【答案】(1)![]() (x≠±2);(2)x±y+1=0.
(x≠±2);(2)x±y+1=0.
【解析】
(1)设点P(x,y),直接把已知条件用坐标表示并化简即可;
(2)设直线AB的方程为x=my﹣1,A(x1,y1),B(x2,y2),由直线与椭圆相交弦长公式(应用韦达定理计算)求出弦长,交求出原点到直线![]() 距离,表示出
距离,表示出![]() 面积,由对称性知四边形ABCD的面积是
面积,由对称性知四边形ABCD的面积是![]() 面积的4倍,从而可以求出
面积的4倍,从而可以求出![]() .
.
解:(1)设点P(x,y),
∵直线PM与PN的斜率之积为﹣![]() ,
,
即![]() =
=![]() =﹣
=﹣![]() ,
,
化简得![]() (x≠±2),
(x≠±2),
∴动点P的轨迹E的方程为![]() (x≠±2);
(x≠±2);
(2)设直线AB的方程为x=my﹣1,A(x1,y1),B(x2,y2),
由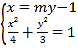
得(3m2+4)y2﹣6my﹣9=0,
则 ![]() , y1+y2=
, y1+y2=![]() ,
,![]() ,
,
|y1﹣y2|=![]() =
=![]() ,
,
∴|AB|=![]() =
=![]() ,
,
又原点O到直线AB的距离d=![]() ,
,
∴S△ABO=![]() ×
×![]() =
=![]() ,
,
由图形的对称性可知,SABCD=4S△ABO,
∴SABCD=![]() =
=![]() ,
,
化简得18m4﹣m2﹣17=0,
解得m2=1,即m=±1,
∴直线AB的方程为x=±y﹣1,即x±y+1=0.


科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.
(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年辽宁省正式实施高考改革.新高考模式下,学生将根据自己的兴趣、爱好、学科特长和高校提供的“选考科目要求”进行选课.这样学生既能尊重自己爱好、特长做好生涯规划,又能发挥学科优势,进而在高考中获得更好的成绩和实现自己的理想.考改实施后,学生将在高二年级将面临着![]() 的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
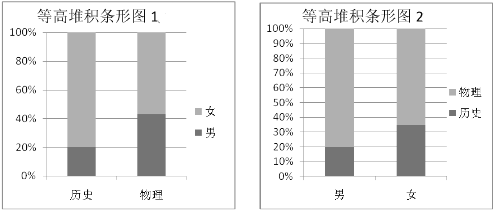
A.样本中的女生数量多于男生数量
B.样本中有学物理意愿的学生数量多于有学历史意愿的学生数量
C.样本中的男生偏爱物理
D.样本中的女生偏爱历史
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线![]() 与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作.其中的一道题“今有木,方三尺,高三尺,欲方五寸作枕一枚.问:得几何?”意思是:“有一块棱长为3尺的正方体方木,要把它作成边长为5寸的正方体枕头,可作多少个?”现有这样的一个正方体木料,其外周已涂上油漆,则从切割后的正方体枕头中任取一块,恰有一面涂上油漆的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,
,![]() 是椭圆上关于原点
是椭圆上关于原点![]() 对称的两个动点,当点
对称的两个动点,当点![]() 的坐标为
的坐标为![]() 时,
时,![]() 的周长恰为
的周长恰为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,且
两点,且![]()
![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“工资条里显红利,个税新政人民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.2019年1月1日实施的个税新政主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.
新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税级数 | 每月应纳税所得额(含税)=收入-个税起征点 | 税率(%) | 每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除 | 税率(%) |
1 | 不超过1500元部分 | 3 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元部分 | 10 | 超过3000元至12000元部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元部分 | 30 | 超过35000元至55000元部分 | 30 |
··· | ··· | ··· | ··· | ··· |
随机抽取某市1000名同一收入层级的![]() 从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等。
从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等。
假设该市该收入层级的![]() 从业者都独自享受专项附加扣除,将预估的该市该收入层级的
从业者都独自享受专项附加扣除,将预估的该市该收入层级的![]() 从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
(1)设该市该收入层级的![]() 从业者2019年月缴个税为
从业者2019年月缴个税为![]() 元,求
元,求![]() 的分布列和期望;
的分布列和期望;
(2)根据新旧个税方案,估计从2019年1月开始,经过多少个月,该市该收入层级的![]() 从业者各月少缴交的个税之和就超过2019年的月收入?
从业者各月少缴交的个税之和就超过2019年的月收入?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知曲线C的极坐标方程为![]() (
(![]() ,a为常数)),过点
,a为常数)),过点![]() 、倾斜角为
、倾斜角为![]() 的直线
的直线![]() 的参数方程满足
的参数方程满足![]() ,(
,(![]() 为参数).
为参数).
(1)求曲线C的普通方程和直线![]() 的参数方程;
的参数方程;
(2)若直线![]() 与曲线C相交于A、B两点(点P在A、B之间),且
与曲线C相交于A、B两点(点P在A、B之间),且![]() ,求
,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com