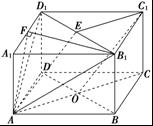
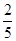(本题满分15分)已知正方体
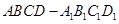
的棱长为1,点
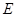
在
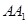
上,点
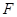
在
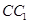
上,且
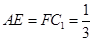
(1)求直线
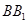
与平面

所成角的余弦值;
(2)用
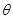
表示平面

和侧面
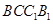
所成的锐二面角的大小,求
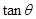
;
(3)若
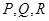
分别在
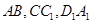
上,并满足
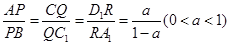
,探索:当
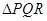
的重心为
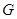
且
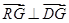
时,求实数
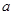
的取值范围.
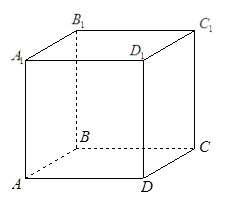
第一问中利用以
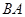
为
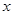
轴,
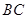
为
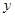
轴,
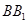
为
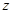
轴建立空间直角坐标系
设
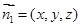
为平面

的法向量,又正方体的棱长为1,
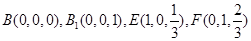
借助于
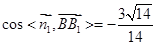
,得到结论
第二问中,
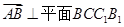
,
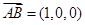
是平面
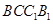
的法向量
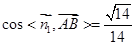
,又平面

和侧面
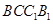
所成的锐二面角为
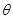

,则
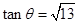
第三问中,因为
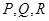
分别在
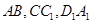
上,且
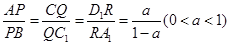
故
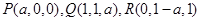
,
所以当
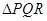
的重心为
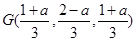
然后利用垂直关系得到结论。
解:(1)以
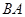
为
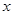
轴,
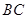
为
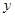
轴,
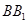
为
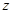
轴建立空间直角坐标系
又正方体的棱长为1,
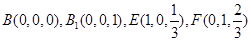
设
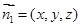
为平面

的法向量

令
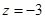
,则
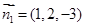
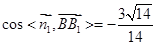
设直线
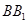
与平面

所成角为
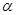
,
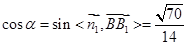
直线
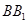
与平面

所成角的余弦值为
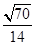
(5分)
(2)
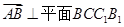
,
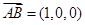
是平面
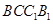
的法向量
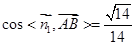
,又平面

和侧面
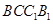
所成的锐二面角为
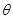

,则
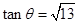
(5分)
(3)因为
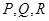
分别在
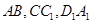
上,且
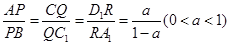
故
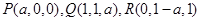
,
所以当
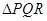
的重心为
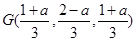
,而
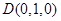
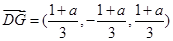
,

当
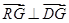
时,
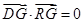

为恒等式
所以,实数
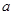
的取值范围为
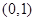
(5分)
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)如图,已知平面

,

是垂足.

(Ⅰ)求证:

平面

;
(Ⅱ)若

,求证:



.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
四面体
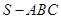
中,各个面都是边长为
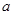
的正三角形,
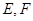
分别是
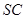
和
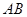
的中 点,则异面直线
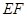
与
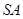
所成的角等于( )
A
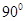
B
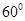
C
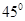
D
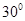
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
正四面体
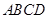
,
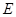
是
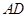
中点,则直线

与直线
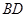
所成的角的余弦值为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在棱长为1的正方体
ABCD-
A1B1C1D1中,
M和
N分别为
A1B1和
BB1的中点,那么直线
AM与
CN所成角的余弦值是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
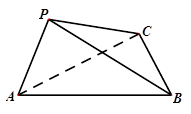
(本小题满分12分)如图,在三棱锥
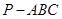
中,
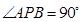
,
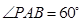
,
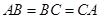
,平面
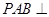
平面
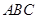
。
(Ⅰ)求直线
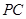
与平面
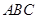
所成角的大小;
(Ⅱ)求二面角
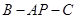
的大小。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图在三棱柱
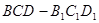
与四棱锥
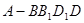
的组合体中,已知
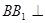
平面
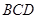
,四边形
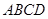
是平行四边形,
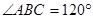
,
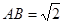
,
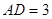
,
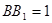
。
(1)设
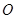
是线段
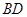
的中点,求证:
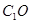
∥平面
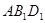
;
(2)求直线
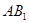
与平面
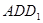
所成的角。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
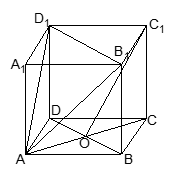
已知正方体ABCD-A
1B
1C
1D
1,
O是底面ABCD对角线的交点.
(1)求证:A
1C⊥平面AB
1D
1;
(2)求
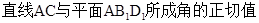
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
如图,在正方体

中,下列结论正确的是( ).

查看答案和解析>>

 的棱长为1,点
的棱长为1,点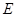 在
在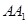 上,点
上,点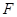 在
在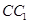 上,且
上,且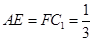
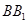 与平面
与平面 所成角的余弦值;
所成角的余弦值;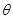 表示平面
表示平面 和侧面
和侧面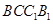 所成的锐二面角的大小,求
所成的锐二面角的大小,求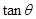 ;
;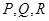 分别在
分别在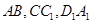 上,并满足
上,并满足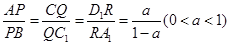 ,探索:当
,探索:当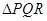 的重心为
的重心为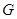 且
且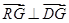 时,求实数
时,求实数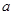 的取值范围.
的取值范围.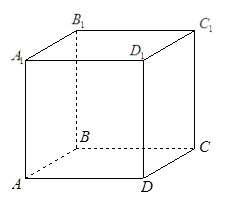
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案