
【题目】将函数y=sin2x的图象向左平移 ![]() 个单位,再向上平移1个单位,所得图象的函数解析式是( )
个单位,再向上平移1个单位,所得图象的函数解析式是( )
A.y=2cos2x
B.y=2sin2x
C.![]()
D.y=cos2x
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() (含端点)上运动,当点
(含端点)上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知AD=PD,PA=6,BC=8,DF=5,求证: 
(1)直线PA∥平面DEF;
(2)平面DEF⊥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:
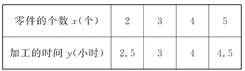
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如图,其中
所在平面互相垂直,如图,其中![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.

(Ⅰ)试问在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?若存在,请证明
?若存在,请证明![]() 平面
平面![]() ,并求出
,并求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取![]() 名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:

(1)求出表中的![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访,再从抽出的这20名中年龄在![]() 的选取2名担任主要发言人.记这2名主要发言人年龄在
的选取2名担任主要发言人.记这2名主要发言人年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岛![]() 上有一座海拔
上有一座海拔![]() 的山峰,山顶设有一个观察站
的山峰,山顶设有一个观察站![]() ,有一艘轮船按一固定方向做匀速直线航行,上午
,有一艘轮船按一固定方向做匀速直线航行,上午![]() 时,测得此船在岛北偏东
时,测得此船在岛北偏东![]() 、俯角为
、俯角为![]() 的
的![]() 处,到
处,到![]() 时,又测得该船在岛北偏西
时,又测得该船在岛北偏西![]() 、俯角
、俯角![]() 为的
为的![]() 处.
处.

(1)求船的航行速度;
(2)求船从![]() 到
到![]() 行驶过程中与观察站
行驶过程中与观察站![]() 的最短距离.
的最短距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com