
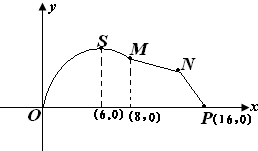
 如图,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数y=Asinωx(A>0,ω>0,x∈[0,8]的图象,且图象的最高点为S(6,4
如图,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数y=Asinωx(A>0,ω>0,x∈[0,8]的图象,且图象的最高点为S(6,4| 3 |
|
|
| 3 |
| π |
| 12 |
|
| (8-16)2+(6-0)2 |
| MN |
| sinθ |
| NP |
| sin(60°-θ) |
| MP |
| sin120° |
| 20 | ||
|
| 20 | ||
|
| 20 | ||
|
| 20 | ||
|
| 20 | ||
|
| 20 | ||
|
20
| ||
| 3 |
| 20 | ||
|
| 20 | ||
|
| 20 | ||
|
| 20 | ||
|
20
| ||
| 3 |


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
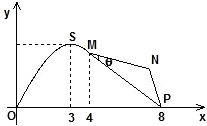 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为S(3,2
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为S(3,2| 3 |
查看答案和解析>>
科目:高中数学 来源:2010年辽宁省鞍山一中高考数学六模试卷(文科)(解析版) 题型:解答题
 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为 ;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120°
;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120°查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省荆州中学高三第二次质量检查数学试卷(文科)(解析版) 题型:解答题
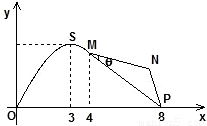 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为 ;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120°
;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120°查看答案和解析>>
科目:高中数学 来源:2009-2010学年高三数学滚动练习试卷(04)(解析版) 题型:解答题
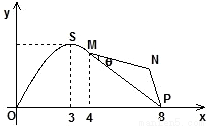 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为 ;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120°
;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com