
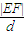 的最大值.并求出此时b的值.
的最大值.并求出此时b的值.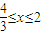 .则问题转化为9x2+6(b-1)x+b2+8=0在区间
.则问题转化为9x2+6(b-1)x+b2+8=0在区间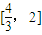 上有两个实根,结合方程的根的分布可求b的范围,根据弦长公式
上有两个实根,结合方程的根的分布可求b的范围,根据弦长公式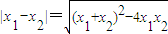 可得
可得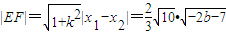 ,再由原点到直线l的距离为
,再由原点到直线l的距离为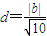 ,,代入结合二次函数的性质可求
,,代入结合二次函数的性质可求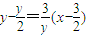 ②
②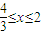 .
.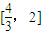 有两个实根.
有两个实根.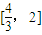 上有两个不等实根的充要条件是
上有两个不等实根的充要条件是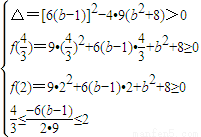
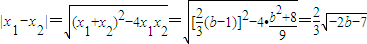
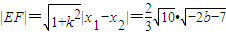
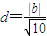 ,
,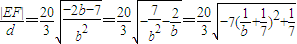
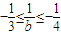 .
.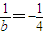 ,即b=-4时,
,即b=-4时,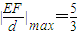 .
.

 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com