
【题目】如图所示,F为双曲线C:![]() ﹣
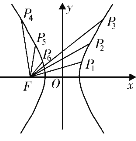
﹣![]() =1的左焦点,双曲线C上的点Pi与P7﹣i(i=1,2,3)关于y轴对称,则|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
=1的左焦点,双曲线C上的点Pi与P7﹣i(i=1,2,3)关于y轴对称,则|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
A. 9 B. 16 C. 18 D. 27
【答案】C
【解析】
首先设右焦点为F′,由点Pi与P7﹣i(i=1,2,3)关于y轴对称以及双曲线的对称性得出|FP1|=|F′P6|,|FP2|=|F′P5|,|FP3|=|F′P4|,然后根据双曲线的定义得出|F′P6|﹣|P6F|=2a=6,|F′P5|﹣|P5F|=2a=6,|F′P4|﹣|P4F|=2a=6,进而求出结果.
设右焦点为F′,
∵双曲线C上的点Pi与P7﹣i(i=1,2,3)关于y轴对称
∴P1和P6,P2和P5,P3和P4分别关于y轴对称
∴|FP1|=|F′P6|,|FP2|=|F′P5|,|FP3|=|F′P4|,
∵|F′P6|﹣|P6F|=2a=6,|F′P5|﹣|P5F|=2a=6,|F′P4|﹣|P4F|=2a=6,
∴|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|=(|F′P6|﹣|P6F|)+(|F′P5|﹣|P5F|)+(|F′P4|﹣|P4F|)=18
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设关于x的一元二次方程![]() ,其中a,b是某范围内的随机数,分别在下列条件下,求上述方程有实根的概率.
,其中a,b是某范围内的随机数,分别在下列条件下,求上述方程有实根的概率.
(1)若随机数a,b∈{1,2,3,4,5,6};
(2)若a是从区间[0,5]中任取的一个数,b是从区间[2,4]中任取的一个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(x+ ![]() )cosx.
)cosx.
(1)若0≤x≤ ![]() ,求函数f(x)的值域;
,求函数f(x)的值域;
(2)设△ABC的三个内角A,B,C所对的边分别为a,b,c,若A为锐角且f(A)= ![]() ,b=2,c=3,求cos(A﹣B)的值.
,b=2,c=3,求cos(A﹣B)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对边的长分别为a,b,c,则下列命题正确的是(写出所有正确命题的编号).
①若ab>c2 , 则C< ![]()
②若a+b>2c,则C< ![]()
③若a3+b3=c3 , 则C< ![]()
④若(a+b)c≤2ab,则C> ![]()
⑤若(a2+b2)c2≤2a2b2 , 则C> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{xn}满足x1=0,xn+1=﹣x2n+xn+c(n∈N*).
(Ⅰ)证明:{xn}是递减数列的充分必要条件是c<0;
(Ⅱ)求c的取值范围,使{xn}是递增数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1是椭圆5x2+9y2=45的左焦点,P为椭圆上半部分任意一点,A(1,1)为椭圆内一点,则|PA|+|PF1|的最小值_______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (α为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin(
(α为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin(![]() )=2
)=2![]() .
.
(Ⅰ)求曲线C和直线l在该直角坐标系下的普通方程;
(Ⅱ)动点A在曲线C上,动点B在直线l上,定点P的坐标为(﹣2,2),求|PB|+|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如图.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm.
(Ⅰ)检查人员从这15条鱼中,随机抽出3条,求3条中恰有1条汞含量超标的概率;
(Ⅱ)若从这批数量很大的鱼中任选3条鱼,记ξ表示抽到的汞含量超标的鱼的条数.以此15条鱼的样本数据来估计这批数量很大的鱼的总体数据,求ξ的分布列及数学期望Eξ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com