已知△ABC中,(b+a)(sinB-sinA)=asinB,又cos2C+cosC=1-cos(A-B).
(I)试判断△ABC的形状;
(II)求cosC的值.
解:(Ⅰ)由cos2C+cosC=1-cos(A-B)
得cosC+cos(A-B)=1-cos2C,cos(A-B)-cos(A+B)=2sin
2C,
即sinAsinB=sin
2C,根据正弦定理,ab=c
2,①,
又由正弦定理及(b+a)(sinB-sinA)=asinB可知b
2-a
2=ab,②,由①②得b
2=a
2+c
2,
所以△ABC是直角三角形,且B=90°;
(Ⅱ)∵A+C=90°,∴sin
2C=sinAsinB=sinA=cosC,
从而cos
2C+cosC-1=0,解得
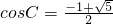
或
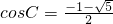
(舍去),
即
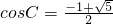
.
分析:(Ⅰ)利用和差化积公式和二倍角公式对cos2C+cosC=1-cos(A-B)整理求得sinAsinB=sin
2C,利用正弦定理换成边的关系,同时利用正弦定理把(b+a)(sinB-sinA)=asinB角的正弦转化成边的问题,然后联立方程求得b
2=a
2+c
2,推断出三角形为直角三角形.
(Ⅱ)利用(1)把sinAsinB=sin
2C整理成关于cosx的一元二次方程求得cosC的值.
点评:本题主要考查了三角形的形状的判断,正弦定理的应用.考查了学生分析问题和解决问题的能力.

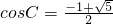 或
或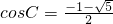 (舍去),
(舍去),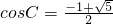 .
.
