已知圆心在直线2x-y-7=0上的圆C与y轴交于两点A(0,-4),B(0,-2);
(1)求圆C的方程.
(2)设点P(x,y)为圆C上的动点,求(x-2)2+y2的取值范围.
【答案】
分析:(1)由题意得到圆心在y=-3上,又圆心在直线2x-y-7=0上,联立求出圆心C坐标,利用两点间的距离公式求出r的值,即可确定出圆C的方程;
(2)法1:由圆C的方程变形代入所求式子化简,表示出Z=-4-6y,由y的范围即可确定出Z的范围;
法2:根据圆的方程设出参数方程,代入所求式子化简,根据sinα的值域即可确定出Z的范围.
解答:解:(1)根据题意知,圆心C在直线y=-3上,
由
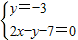
,解得:
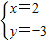
,即圆心C(2,-3),
又r=|AC|=
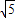
,
则所求圆的方程为:(x-2)
2+(y+3)
2=5;
(2)法1:由圆C方程:(x-2)
2+(y+3)
2=5知:Z=(x-2)
2+y
2=5-(y+3)
2+y
2=-4-6y,
由圆方程知:y∈[-3-
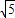
,-3+
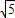
],即-4-6y∈[14-6
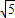
,14+6
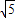
],
则Z∈[14-6
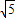
,14+6
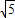
];
法2:由圆C的方程为:(x-2)
2+(y+3)
2=5,
设P(x,y),可得
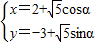
(α为参数,α∈[0,2π]),
代入Z=(x-2)
2+y
2化简得:Z=14-6
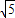
sinα,
∵|sinα|≤1,
∴Z∈[14-6
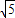
,14+6
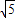
].
点评:此题考查了直线与圆相交的性质,涉及的知识有:圆的标准方程,圆的参数方程,正弦函数的定义域与值域,弄清题意是解本题的关键.

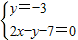 ,解得:
,解得: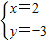 ,即圆心C(2,-3),
,即圆心C(2,-3),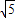 ,
,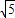 ,-3+
,-3+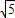 ],即-4-6y∈[14-6
],即-4-6y∈[14-6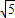 ,14+6
,14+6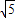 ],
],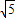 ,14+6
,14+6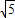 ];
];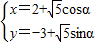 (α为参数,α∈[0,2π]),
(α为参数,α∈[0,2π]),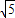 sinα,
sinα,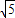 ,14+6
,14+6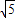 ].
].

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案