
ŅŃÖŖŗÆŹż =
= .
.
(¢ń)µ± Ź±£¬Ēó²»µČŹ½
Ź±£¬Ēó²»µČŹ½
 ”Ż3µÄ½ā¼Æ£»
”Ż3µÄ½ā¼Æ£»
(¢ņ) Čō ”Ü
”Ü µÄ½ā¼Æ°üŗ¬
µÄ½ā¼Æ°üŗ¬ £¬Ēó
£¬Ēó µÄȔֵ·¶Ī§.
µÄȔֵ·¶Ī§.
”¾ĆüĢāŅāĶ¼”æ±¾ĢāÖ÷ŅŖæ¼²éŗ¬¾ų¶ŌÖµ²»µČŹ½µÄ½ā·Ø£¬ŹĒ¼ņµ„Ģā.
”¾½āĪö”æ(¢ń)µ± Ź±£¬
Ź±£¬ =
= £¬
£¬
µ± ”Ü2Ź±£¬ÓÉ
”Ü2Ź±£¬ÓÉ ”Ż3µĆ
”Ż3µĆ £¬½āµĆ
£¬½āµĆ ”Ü1£»
”Ü1£»
µ±2£¼ £¼3Ź±£¬
£¼3Ź±£¬ ”Ż3£¬ĪŽ½ā£»
”Ż3£¬ĪŽ½ā£»
µ± ”Ż3Ź±£¬ÓÉ
”Ż3Ź±£¬ÓÉ ”Ż3µĆ
”Ż3µĆ ”Ż3£¬½āµĆ
”Ż3£¬½āµĆ ”Ż8£¬
”Ż8£¬
”ą ”Ż3µÄ½ā¼ÆĪŖ{
”Ż3µÄ½ā¼ÆĪŖ{ |
| ”Ü1»ņ
”Ü1»ņ ”Ż8}£»
”Ż8}£»
(¢ņ)  ”Ü
ӆ
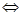
 £¬
£¬
µ± ”Ź[1,2]Ź±£¬
”Ź[1,2]Ź±£¬ =
= =2£¬
=2£¬
”ą £¬ÓŠĢõ¼žµĆ
£¬ÓŠĢõ¼žµĆ ĒŅ
ĒŅ £¬¼“
£¬¼“ £¬
£¬
¹ŹĀś×ćĢõ¼žµÄ µÄȔֵ·¶Ī§ĪŖ[£3,0]
µÄȔֵ·¶Ī§ĪŖ[£3,0]

| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 3 |
| ¦Š |
| 24 |
| 5¦Š |
| 24 |
| ¦Š |
| 24 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 11¦Š |
| 6 |
| ||
| 2 |
| 3 |
| ¦Š |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| xn+2 | xn-2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 ŅŃÖŖŗÆŹżf£Øx£©=Asin£Ø¦Ųx+¦Õ£©£ØA£¾0£¬¦Ų£¾0£¬|¦Õ|£¼
ŅŃÖŖŗÆŹżf£Øx£©=Asin£Ø¦Ųx+¦Õ£©£ØA£¾0£¬¦Ų£¾0£¬|¦Õ|£¼| ¦Š |
| 2 |
AӢf(x)=2sin(
| ||||
BӢf(x)=2sin(
| ||||
CӢf(x)=2sin(2x-
| ||||
DӢf(x)=2sin(2x+
|
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com