
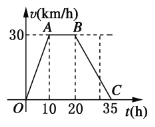
【题目】据气象中心观察和预测:发生于甲地的沙尘暴一直向正南方向移动,其移动速度![]() 与时间
与时间![]() 的函数图象图所示,过线段
的函数图象图所示,过线段![]() 上一点
上一点![]() 作横轴的垂线
作横轴的垂线![]() ,梯形
,梯形![]() 在直线
在直线![]() 左侧部分的面积即为
左侧部分的面积即为![]() 内沙尘暴所经过的路程
内沙尘暴所经过的路程![]() .
.
(1) 当![]() 时,求
时,求![]() 的值;
的值;
(2)将![]() 随
随![]() 变化的规律用数学关系式表示出来;
变化的规律用数学关系式表示出来;
(3)若乙城位于甲地正南方向,且距甲地![]() ,试判断这场沙尘暴是否会侵袭到乙城,如果会,在沙尘暴发生后多长时间它将侵袭到乙城?如果不会,请说明理由.
,试判断这场沙尘暴是否会侵袭到乙城,如果会,在沙尘暴发生后多长时间它将侵袭到乙城?如果不会,请说明理由.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】给出以下关于线性方程组解的个数的命题.
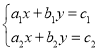 ①,
①,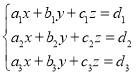 ②,
②,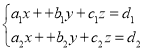 ③,
③, ④,
④,
(1)方程组①可能有无穷多组解;
(2)方程组②可能有且只有两组不同的解;
(3)方程组③可能有且只有唯一一组解;
(4)方程组④可能有且只有唯一一组解.
其中真命题的序号为________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 同时满足:①对于任意的正整数
同时满足:①对于任意的正整数![]() ,
, ![]() 恒成立;②对于给定的正整数
恒成立;②对于给定的正整数![]() ,
, ![]() 对于任意的正整数
对于任意的正整数![]() 恒成立,则称数列
恒成立,则称数列![]() 是“
是“![]() 数列”.
数列”.
(1)已知![]() 判断数列
判断数列![]() 是否为“
是否为“![]() 数列”,并说明理由;
数列”,并说明理由;
(2)已知数列![]() 是“
是“![]() 数列”,且存在整数
数列”,且存在整数![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等差数列,证明:
成等差数列,证明: ![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心C在直线![]() 上的圆过两点
上的圆过两点![]() ,
,![]() .
.
(1)求圆C的方程;
(2)若直线![]() 与圆C相交于A,B两点,①当
与圆C相交于A,B两点,①当![]() 时,求AB的方程;②在y轴上是否存在定点M,使
时,求AB的方程;②在y轴上是否存在定点M,使![]() ,若存在,求出M的坐标;若不存在,说明理由.
,若存在,求出M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() ,
,![]() 满足:对任意正整数
满足:对任意正整数![]() ,都有
,都有![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,
,![]() ,
,![]() 成等比数列,且
成等比数列,且![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅲ)设![]() =
=![]() +
+![]() +…+
+…+![]() ,如果对任意的正整数
,如果对任意的正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆![]() .
.
(1)若椭圆![]() ,判断
,判断![]() 与
与![]() 是否相似?如果相似,求出
是否相似?如果相似,求出![]() 与
与![]() 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
(2)写出与椭圆![]() 相似且焦点在
相似且焦点在![]() 轴上、短半轴长为
轴上、短半轴长为![]() 的椭圆
的椭圆![]() 的标准方程;若在椭圆
的标准方程;若在椭圆![]() 上存在两点
上存在两点![]() 、
、![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围;
的取值范围;
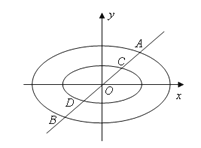
(3)如图:直线![]() 与两个“相似椭圆”
与两个“相似椭圆”![]() 和
和![]() 分别交于点
分别交于点![]() 和点
和点![]() ,试在椭圆
,试在椭圆![]() 和椭圆
和椭圆![]() 上分别作出点
上分别作出点![]() 和点
和点![]() (非椭圆顶点),使
(非椭圆顶点),使![]() 和
和![]() 组成以
组成以![]() 为相似比的两个相似三角形,写出具体作法.(不必证明)
为相似比的两个相似三角形,写出具体作法.(不必证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学在高二下学期开设四门数学选修课,分别为《数学史选讲》.《球面上的几何》.《对称与群》.《矩阵与变换》.现有甲.乙.丙.丁四位同学从这四门选修课程中选修一门,且这四位同学选修的课程互不相同,下面关于他们选课的一些信息:①甲同学和丙同学均不选《球面上的几何》,也不选《对称与群》:②乙同学不选《对称与群》,也不选《数学史选讲》:③如果甲同学不选《数学史选讲》,那么丁同学就不选《对称与群》.若这些信息都是正确的,则丙同学选修的课程是( )
A. 《数学史选讲》B. 《球面上的几何》C. 《对称与群》D. 《矩阵与变换》
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com