
解析:(1)当a=-2,b=-8时,所给不等式左边=x2+ax+b|=|x2-2x-8|≤2|x2-2x-8|=|2x2-4x-16|=右边
∴此时所给不等式对一切x∈R成立
(2)注意到 2x2-4x-16=0![]() x2-2x-8=0
x2-2x-8=0![]() (x+2)(x-4)=0
(x+2)(x-4)=0![]() x=-2或x=4 ∴当x=-2或x=4时 |2x2-4x-16|=0
x=-2或x=4 ∴当x=-2或x=4时 |2x2-4x-16|=0
∴在不等式|x2+ax+b|≤|2x2-4x-16|中分别取x=-2,x=4得 ![]()
又注意到(1)知当a=-2,b=-8时,所给不等式互对一切x![]() R均成立。∴满足题意的实数a,b只能a=-2,b=-8一组
R均成立。∴满足题意的实数a,b只能a=-2,b=-8一组
(3)由已知不等式x2-2x-8≥(m+2)x-m-15


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
A.|a+b|>|a-b| B.|a+b|<|a-b|
C.|a-b|<||a|-|b|| D.|a-b|<|a|+|b|
查看答案和解析>>
科目:高中数学 来源: 题型:
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省郑州市高三第十四次调考理科数学试卷(解析版) 题型:填空题
已知实数a,b满足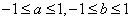 ,则函数f(x)=
,则函数f(x)= 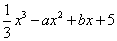 的两个极值点都在(0,1)内的概率为______
的两个极值点都在(0,1)内的概率为______
查看答案和解析>>
科目:高中数学 来源:2010-2011学年西藏拉萨中学高三第六模拟考试数学理卷 题型:选择题
已知实数a,b满足a+2b=1,则2a+4b的最小值是
A.2
B.2 C.4
D.4
C.4
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com