
【题目】某工厂生产了一批零件,从中随机抽取100个作为样本,测出它们的长度(单位:厘米),按数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 5组,得到如图所示的频率分布直方图.以这100个零件的长度在各组的频率代替整批零件长度在该组的概率.
5组,得到如图所示的频率分布直方图.以这100个零件的长度在各组的频率代替整批零件长度在该组的概率.

(1)估计该工厂生产的这批零件长度的平均值(同一组中的每个数据用该组区间的中点值代替);
(2)若用分层抽样的方式从第1组和第5组中抽取5个零件,再从这5个零件中随机抽取2个,求抽取的零件中恰有1个是第1组的概率.
【答案】(1)23.1;(2)![]() .
.
【解析】
(1)根据频率分布直方图得到各组频率,然后由平均数公式求解.
(2)由题意可知第1组和第5组的零件数分别是8和12,利用分层抽样得到应从第1组中抽取2个零件,从第5组中抽取3个零件,然后再利用古典概型的概率求法求解.
(1)由频率分布直方图可得各组频率依次为![]() ,
,
则这批零件长度的平均值为
![]() .
.
(2)由题意可知第1组和第5组的零件数分别是8和12,
则应从第1组中抽取2个零件,记为A,B;
应从第5组中抽取3个零件,记为c,d,e.
从这5个零件中随机抽取2个的情况有AB,Ac,Ad,Ae,Bc,Bd,Be,cd,ce,de,共10种,
其中符合条件的情况有Ac,Ad,Ae,Bc,Bd,Be,共6种.
故所求概率![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】已知空间中两条直线![]() ,
,![]() 所成的角为50°,
所成的角为50°,![]() 为空间中给定的一个点,直线
为空间中给定的一个点,直线![]() 过点
过点![]() 且与直线
且与直线![]() ,
,![]() 所成的角都是
所成的角都是![]() ,则下列判断中正确的是( )
,则下列判断中正确的是( )
①当![]() 时,满足题意的直线
时,满足题意的直线![]() 不存在;②当
不存在;②当![]() 时,满足题意的直线
时,满足题意的直线![]() 有且只有1条;③当
有且只有1条;③当![]() 时,满足题意的直线
时,满足题意的直线![]() 有且只有2条;④当
有且只有2条;④当![]() 时,满足题意的直线
时,满足题意的直线![]() 有且只有3条.
有且只有3条.
A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)当a=1 时,求不等式f(x)≤5的解集;
(2)x0∈R,f(x0)≤|2a+1|,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在北宋年间(公元1084年)第一次印刷出版了《算经十书》,即贾宪的《黄帝九章算法细草》,刘益的《议古根源》,秦九韶的《数书九章》,李冶的《测圆海镜》和《益古演段》,杨辉的《详解九章算法》、《日用算法》和《杨辉算法》,朱世杰的《算学启蒙》和《四元玉鉴》.这些书中涉及的很多方面都达到古代数学的高峰,其中一些“算法”如开立方和开四次方也是当时世界数学的高峰,哈三中图书馆中正好有这十本书,但是书名中含有“算”字的书都已经借出,现在小张同学从剩余的书中任借两本阅读,那么他借到《数书九章》的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】稠环芳香烃化合物中有不少是致癌物质,比如学生钟爱的快餐油炸食品中会产生苯并芘,它是由一个苯环和一个芘分子结合而成的稠环芳香烃类化合物,长期食用会致癌.下面是一组稠环芳香烃的结构简式和分子式:
名称 | 萘 | 蒽 | 并四苯 | … | 并n苯 |
结构简式 |
|
|
| … | … |
分子式 |
|
|
| … | … |
由此推断并十苯的分子式为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系![]() 坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是
坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是![]() .
.
(1)求曲线C直角坐标方程;
(2)射线![]() 与曲线C相交于点
与曲线C相交于点![]() ,直线
,直线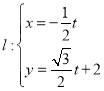 (t为参数)与曲线C相交于点D,E,求
(t为参数)与曲线C相交于点D,E,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款小游戏的规则如下:每轮游戏要进行三次,每次游戏都需要从装有大小相同的2个红球,3个白球的袋中随机摸出2个球,若摸出的“两个都是红球”出现3次获得200分,若摸出“两个都是红球”出现1次或2次获得20分,若摸出“两个都是红球”出现0次则扣除10分(即获得![]() 分).
分).
(1)设每轮游戏中出现“摸出两个都是红球”的次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩过这款游戏的许多人发现,若干轮游戏后,与最初的分数相比,分数没有增加反而减少了,请运用概率统计的相关知识分析解释上述现象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com