
【题目】甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.
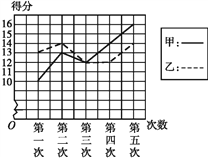
(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩作出评价.
【答案】(1)![]() ;
;
(2)乙的成绩较稳定,甲的成绩在不断提高,而乙的成绩则无明显提高
【解析】试题分析:(1)由图象可得甲、乙两人五次测试的成绩分别为,甲:10分,13分,12分,14分,16分;乙:13分,14分,12分,12分,14分.根据平均数,方差的公式代入计算得解(2) 由![]() 可知乙的成绩较稳定.从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,可知甲的成绩在不断提高,而乙的成绩则无明显提高.
可知乙的成绩较稳定.从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,可知甲的成绩在不断提高,而乙的成绩则无明显提高.
试题解析:
(1)由图象可得甲、乙两人五次测试的成绩分别为
甲:10分,13分,12分,14分,16分;
乙:13分,14分,12分,12分,14分.
![]() =13,
=13,
![]() =13,
=13,
![]() ×[(10-13)2+(13-13)2+(12-13)2+(14-13)2+(16-13)2]=4,
×[(10-13)2+(13-13)2+(12-13)2+(14-13)2+(16-13)2]=4,
![]() ×[(13-13)2+(14-13)2+(12-13)2+(12-13)2+(14-13)2]=0.8.
×[(13-13)2+(14-13)2+(12-13)2+(12-13)2+(14-13)2]=0.8.
(2)由![]() 可知乙的成绩较稳定.
可知乙的成绩较稳定.
从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,可知甲的成绩在不断提高,而乙的成绩则无明显提高.


科目:高中数学 来源: 题型:
【题目】在极坐标系下,已知曲线C1:ρ=cosθ+sinθ和曲线C2:ρsin(θ﹣ ![]() )=
)= ![]() .
.
(1)求曲线C1和曲线C2的直角坐标方程;
(2)当θ∈(0,π)时,求曲线C1和曲线C2公共点的一个极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2﹣lnx﹣2.
ax2﹣lnx﹣2.
(1)当a=1时,求曲线f(x)在点(1,f(1))处的切线方程;
(2)若a>0,求函数f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x/万元 | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y/万元 | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根据上表可得回归直线方程![]() x+
x+![]() ,其中
,其中![]() =0.76,
=0.76, ![]() ,据此估计,该社区一户居民年收入为15万元家庭的年支出为_____万元.
,据此估计,该社区一户居民年收入为15万元家庭的年支出为_____万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (e是自然对数的底数),h(x)=1﹣x﹣xlnx.
(e是自然对数的底数),h(x)=1﹣x﹣xlnx.
(1)求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求h(x)的单调区间;
(3)设g(x)=xf′(x),其中f′(x)为f(x)的导函数,证明:对任意x>0,g(x)<1+e﹣2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,因此必须掌握钢水含碳量和冶炼时间的关系.如果已测得炉料熔化完毕时,钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出钢的时间)的一些数据,如下表所示:
x/0.01% | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
y/min | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
(1)作出散点图,你能从散点图中发现含碳量与冶炼时间的一般规律吗?
(2)求回归直线方程.
(3)预测当钢水含碳量为160时,应冶炼多少分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com