
分析 利用利用诱导公式求得tanθ的值,再利用诱导公式、同角三角函数的基本关系求得要求式子的值.
解答 解:若$cot({\frac{3π}{2}-θ})=\frac{1}{2}$=tanθ,
则$\frac{{sin({3π-θ})+sin({\frac{3}{2}π+θ})}}{{cos({\frac{π}{2}+θ})+cos({π-θ})}}$=$\frac{sinθ-cosθ}{-sinθ-cosθ}$=$\frac{cosθ-sinθ}{cosθ+sinθ}$=$\frac{1-tanθ}{1+tanθ}$=$\frac{\frac{1}{2}}{\frac{3}{2}}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题主要考查利用诱导公式、同角三角函数的基本关系进行化简求值,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
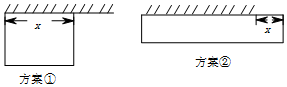 上海市复兴高级中学二期改扩建工程于2015年9月正式开始,现需要围建一个面积火900平方米的矩形地场地的围墙,有一面长度为20米的旧墙(图中斜杠部),有甲、乙两种维修利用旧墙方案.
上海市复兴高级中学二期改扩建工程于2015年9月正式开始,现需要围建一个面积火900平方米的矩形地场地的围墙,有一面长度为20米的旧墙(图中斜杠部),有甲、乙两种维修利用旧墙方案.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com