练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数(其中0<<1,),且的图象在y轴右侧的第一个最高点横坐标为，且在区间上的最小值为，则a=(    )

    A．1                B．2                C．          D．

     

    【答案】

    D

    【解析】

    试题分析：既然在处取得第一个最高点，那么有2×+=,=

    所以,f(x)=sin(x+)+a+,f(x)在区间上的最小值为,

    当x在区间时，x+在区间[0,]里，在这个区间内，当x+=时，取得最小值。即此时f(x)的最小值为a+-=，故有,选D.

    考点：正弦型函数的图象和性质

    点评：中档题，关键是确定角的范围，进一步求得三角函数值的范围，得到a的方程。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014届黑龙江省高一上学期期末考试数学试卷 题型：解答题

    (本题满分12分)设函数f(x)＝a·b，其中向量a＝(2cosx,1)，b＝(cosx，sin2x＋m)．

    (1)求函数f(x)的最小正周期和在[0，π]上的单调递增区间．

    (2)当x∈时，－4<f(x)<4恒成立，求实数m的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2013届江西省高二上学期第二次月考理科数学试卷 题型：填空题

    下列四个命题中

    ①从匀速传递的产品生产流水线上，质检员每20分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样。

    ②由y=3sin2x的图像向右平移个单位长度可以得到函数的图像。

    ③在回归直线方程y=0.2x+12中，当变量x每增加一个单位时，变量y增加0.2个单位。

    ④设0<x<是的充分而不必要条件。

    其中假命题是       （将你认为是假命题的序号都填上）

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数，设，，，其中0<c<b<a<1，那

       么x、y、z的大小顺序为_________。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数其中a<0,且a≠-1．

    （Ⅰ）讨论函数的单调性；

    （Ⅱ）设函数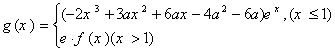（e是自然对数的底数），是否存在a，使在[a,-a]上为减函数？若存在，求a的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案