
已知函数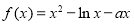 ,
, .
.
(1)若存在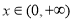 ,使得
,使得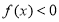 ,求a的取值范围;
,求a的取值范围;
(2)若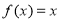 有两个不同的实数解
有两个不同的实数解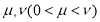 ,证明:
,证明: .
.
(1)(1,+∞);(2)证明过程详见解析.
【解析】
试题分析:本题考查导数的运算、利用导数判断函数的单调性、利用导数求函数最值、恒成立问题等基础知识,考查学生分析问题解决问题的能力、转化能力、计算能力.第一问,先将已知不等式进行转化,将所求的参数分离出来,构造新的函数,利用“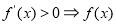 单调递增,
单调递增,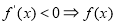 单调递减”判断函数的单调性,确定函数最值的位置,并求出函数的最值,代入到所转化的式子中即可;第二问,将方程的2个根分别代入到方程中,得到2个式子,2个式子作差,得到方程将a分离出来,对
单调递减”判断函数的单调性,确定函数最值的位置,并求出函数的最值,代入到所转化的式子中即可;第二问,将方程的2个根分别代入到方程中,得到2个式子,2个式子作差,得到方程将a分离出来,对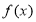 求导,将
求导,将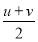 代入,将上述的a也代入,得到所求式子的左边,只需证明
代入,将上述的a也代入,得到所求式子的左边,只需证明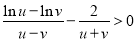 即可,通过变形,只需证明
即可,通过变形,只需证明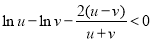 即可,构造新函数
即可,构造新函数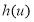 ,所以利用导数求函数的最小值,判断
,所以利用导数求函数的最小值,判断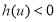 ,即
,即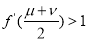 .
.
试题解析:(1)当x∈(0,+∞)时,f(x)<0等价于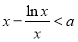 .
.
令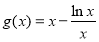 ,则
,则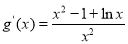 ,
,
当x∈(0,1)时,g?(x)<0;当x∈(1,+∞)时,g?(x)>0.
g(x)有最小值g(1)=1. 4分
故a的取值范围是(1,+∞). 5分
(2)因f(x)=x,即x2-lnx=(a+1)x有两个不同的实数解u,v.
故u2-lnu=(a+1)u,v2-lnv=(a+1)v.
于是(u+v)(u-v)-(lnu-lnv)=(a+1)(u-v). 7分
由u-v<0解得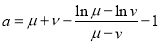 .
.
又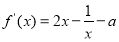 ,所以
,所以
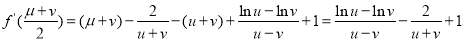 . 9分
. 9分
设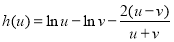 ,则当u∈(0,v)时,
,则当u∈(0,v)时,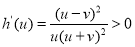 ,
,
h(u)在(0,v)单调递增,h(u)<h(v)=0,
从而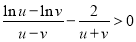 ,因此
,因此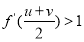 . 12分
. 12分
考点:导数的运算、利用导数判断函数的单调性、利用导数求函数最值、恒成立问题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:2013-2014学年河北省高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题:

(1)求参加数学抽测的人数 、抽测成绩的中位数及分数分别在
、抽测成绩的中位数及分数分别在 ,
, 内的人数;
内的人数;
(2)若从分数在 内的学生中任选两人进行调研谈话,求恰好有一人分数在
内的学生中任选两人进行调研谈话,求恰好有一人分数在 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理科数学试卷(解析版) 题型:选择题
若p: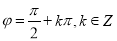 ,q:f(x)=sin(
,q:f(x)=sin(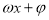 )(
)(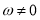 )是偶函数,则p是q的( )
)是偶函数,则p是q的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理文数学试卷(解析版) 题型:选择题
在△ABC中,角A,B,C所对的边长分别为a,b,c,且满足csinA= acosC,则sinA+sinB的最大值是()
acosC,则sinA+sinB的最大值是()
A.1 B. C.
C. D.3
D.3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理文数学试卷(解析版) 题型:选择题
设不等式x2-x≤0的解集为M,函数f(x)=lg(1-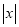 )的定义域为N,则
)的定义域为N,则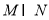 =()
=()
A.(-1,0]
B.[0,1)
C.[0,1]
D.(0,1)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第二次模拟考试理科数学试卷(解析版) 题型:选择题
某几何体的三视图如图所示,则该几何体的体积为( )
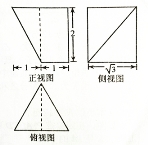
A. B.
B.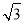 C.
C.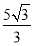 D.
D.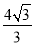
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试文科数学试卷(解析版) 题型:解答题
已知曲线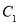 的直角坐标方程为
的直角坐标方程为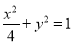 . 以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. P是曲线
. 以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系. P是曲线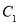 上一点,
上一点,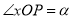 ,
, ,将点P绕点O逆时针旋转角
,将点P绕点O逆时针旋转角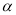 后得到点Q,
后得到点Q,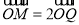 ,点M的轨迹是曲线
,点M的轨迹是曲线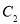 .
.
(1)求曲线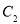 的极坐标方程;
的极坐标方程;
(2)求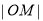 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com