
分析 (1)由f(x)=ax为单调函数,即有a-1+a=$\frac{5}{2}$,即可得到a的值;
(2)化简不等式可得-1≤1+b•2x-b2•2-x≤1,运用换元法和指数函数的单调性,结合二次函数的性质,解不等式即可得到所求范围.
解答 解:(1)函数f(x)=ax为单调函数,
即有a-1+a=$\frac{5}{2}$,解得a=2或$\frac{1}{2}$;
(2)a>1,且不等式|$\frac{f(x)+bg(x)}{f(x)}$|≤1在x∈[0,1]恒成立,
即为|1+b•2x-b2•2-x|≤1,即为-1≤1+b•2x-b2•2-x≤1,
即b•2x-b2•2-x≤0,即为2x≥b•2-x,(b<0)显然成立;
又2+b•2x-b2•2-x≥0在[0,1]恒成立,
令t=2x(1≤t≤2),可得bt2+2t-b2≥0,
由b<0,可得-bt2-2t+b2≤0,在[1,2]恒成立,
即有$\left\{\begin{array}{l}{-b-2+{b}^{2}≤0}\\{-4b-4+{b}^{2}≤0}\end{array}\right.$,即为$\left\{\begin{array}{l}{-1≤b≤2}\\{2-2\sqrt{2}≤b≤2+2\sqrt{2}}\end{array}\right.$,
可得2-2$\sqrt{2}$≤b<0,
则b的取值范围是[2-2$\sqrt{2}$,0).
点评 本题考查指数函数的单调性的运用,同时考查不等式恒成立问题的解法,注意转化思想的运用和二次函数的性质,考查运算能力,属于中档题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
| A. | k<2 | B. | k≤2 | C. | .0≤k<2 | D. | 0≤k≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. | 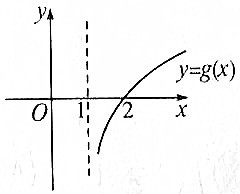 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$,M是棱PC上一点,PA∥平面MOB;
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$,M是棱PC上一点,PA∥平面MOB; 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com