
【题目】某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为
,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为![]() .
.
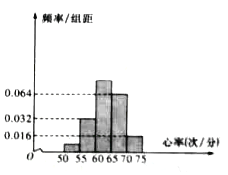
(Ⅰ)求![]() 的值,并求这50名同学心率的平均值;
的值,并求这50名同学心率的平均值;
(Ⅱ)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?说明你的理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 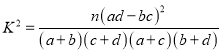 ,其中
,其中![]()
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计 | 50 |
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(1)求出各组的频数,即可求a的值和50名同学的心率平均值.
(2)列出二联表,代入公式求![]() 做出判断即可.
做出判断即可.
试题解析:
(Ⅰ)因为第二组数据的频率为![]() ,故第二组的频数为
,故第二组的频数为![]() ,所以第一组的频数为
,所以第一组的频数为![]() ,第三组的频数为20,第四组的频数为16,第五组的数为4.所以
,第三组的频数为20,第四组的频数为16,第五组的数为4.所以![]()
![]() ,故
,故![]() .
.
这50名同学的心率平均值为![]()
![]()
![]() .
.
(Ⅱ)由(Ⅰ)知,第一组和第二组的学生(即心率小于60次/分的学生)共10名,从而体育生有![]() 名,故列联表补充如下.
名,故列联表补充如下.
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 8 | 12 | 20 |
艺术生 | 2 | 28 | 30 |
合计 | 10 | 40 | 50 |
所以![]()
![]() ,
,
故有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
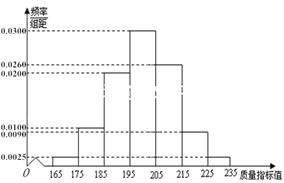
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定?
(Ⅱ)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(Ⅲ)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
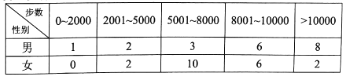
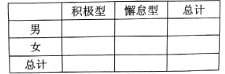
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 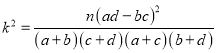 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x∈R),给出下面四个命题:
(x∈R),给出下面四个命题:
①函数f(x)的图象一定关于某条直线对称;
②函数f(x)在R上是周期函数;
③函数f(x)的最大值为 ![]() ;
;
④对任意两个不相等的实数 ![]() ,都有
,都有 ![]() 成立.
成立.
其中所有真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设要抽查某企业生产的某种品牌的袋装牛奶的质量是否达标,现从700袋牛奶中抽取50袋进行检验,利用随机数表抽取样本时,先将700袋牛奶按001,002,…,700进行编号,如果从随机数表第3行第1组开始向右读,最先读到的5袋牛奶的编号是614,593,379,242,203,请你以此方式继续向右读数,随后读出的3袋牛奶的编号是________.(下列摘取了随机数表第1行至第5行)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() (p、q为常数,
(p、q为常数, ![]() ),又
),又![]() ,
, ![]() ,
, ![]() .
.
(1)求p、q的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在正整数m、n,使![]() 成立?若存在,求出所有符合条件的有序实数对
成立?若存在,求出所有符合条件的有序实数对![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(2ωx+ ![]() )(其中ω>0),且f(x)的图象在y轴右侧的第一个最高点的横坐标是
)(其中ω>0),且f(x)的图象在y轴右侧的第一个最高点的横坐标是 ![]() .
.
(1)求y=f(x)的最小正周期及对称轴;
(2)若x∈ ![]() ,函数
,函数 ![]() ﹣af(x)+1的最小值为0.求a的值.
﹣af(x)+1的最小值为0.求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题12分)已知平行四边形![]() 的三个顶点的坐标为
的三个顶点的坐标为![]() ,
,![]() ,
,![]() .
.
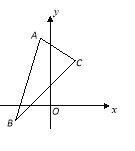
(Ⅰ)在![]() ABC中,求边AC中线所在直线方程;
ABC中,求边AC中线所在直线方程;
(Ⅱ)求平行四边形![]() 的顶点D的坐标及边BC的长度;
的顶点D的坐标及边BC的长度;
(Ⅲ)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com