
【题目】已知函数f(x)=2cosx(sinx﹣cosx)+1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间 ![]() 上的最小值和最大值.
上的最小值和最大值.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga ![]() (a>0,a≠1)是奇函数.
(a>0,a≠1)是奇函数.
(1)求实数m的值;
(2)当x∈(n,a﹣2)时,函数f(x)的值域是(1,+∞),求实数a与n的值;
(3)设函数g(x)=﹣ax2+8(x﹣1)af(x)﹣5,a≥8时,存在最大实数t,使得x∈(1,t]时﹣5≤g(x)≤5恒成立,请写出t与a的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为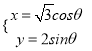 (
(![]() 为参数).以平面直角坐标系
为参数).以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,取相同的单位长度建立极坐标系,直线
轴正半轴为极轴,取相同的单位长度建立极坐标系,直线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)试写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斜三棱柱A1B1C1﹣ABC中,侧面AA1C1C⊥底面ABC,侧面AA1C1C是菱形,∠A1AC=60°,AC=3,AB=BC=2,E、F分别是A1C1 , AB的中点. 
(1)求证:EF∥平面BB1C1C;
(2)求证:CE⊥面ABC.
(3)求四棱锥E﹣BCC1B1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲乙两班各6名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图,则甲班样本数据的众数和乙班样本数据的中位数分别是( ) 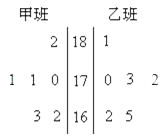
A.170,170
B.171,171
C.171,170
D.170,172
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}是等差数列,首项a1>0,a2003+a2004>0,a2003 . a2004<0,则使前n项和Sn>0成立的最大自然数n是( )
A.4005
B.4006
C.4007
D.4008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是:( )
A. 命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”
”
B. 命题“存在![]() ,使得
,使得![]() ”的否定是:“任意
”的否定是:“任意![]() ,都有
,都有![]() ”
”
C. 若命题“非![]() ”与命题“
”与命题“![]() 或
或![]() ”都是真命题,那么命题
”都是真命题,那么命题![]() 一定是真命题
一定是真命题
D. 命题“若![]() ,则
,则![]() ”的逆命题是真命题
”的逆命题是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com