
科目:高中数学 来源:2013-2014学年上海市杨浦区高三上学期学业质量调研理科数学试卷(解析版) 题型:解答题
设 是数列
是数列 的前
的前 项和,对任意
项和,对任意 都有
都有 成立, (其中
成立, (其中 、
、 、
、 是常数).
是常数).
(1)当 ,
, ,
, 时,求
时,求 ;
;
(2)当 ,
, ,
, 时,
时,
①若 ,
,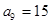 ,求数列
,求数列 的通项公式;
的通项公式;
②设数列 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“ 数列”.
数列”.
如果 ,试问:是否存在数列
,试问:是否存在数列 为“
为“ 数列”,使得对任意
数列”,使得对任意 ,都有
,都有
 ,且
,且 .若存在,求数列
.若存在,求数列 的首项
的首项 的所
的所
有取值构成的集合;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届江西省红色六校高三第一次联考理科数学试卷(解析版) 题型:解答题
对于任意的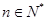 (
(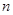 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前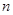 项和等于该数列的前
项和等于该数列的前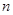 项之积,则称该数列为
项之积,则称该数列为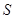 型数列。
型数列。
(1)若数列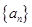 是首项
是首项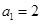 的
的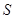 型数列,求
型数列,求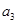 的值;
的值;
(2)证明:任何项数不小于3的递增的正整数列都不是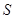 型数列;
型数列;
(3)若数列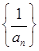 是
是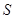 型数列,且
型数列,且 试求
试求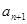 与
与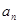 的递推关系,并证明
的递推关系,并证明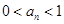 对
对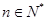 恒成立。
恒成立。
查看答案和解析>>
科目:高中数学 来源:2014届河北省高一下学期期末数学试卷(解析版) 题型:填空题
若一个数列的第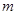 项等于这个数列的前
项等于这个数列的前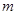 项和,则称该数列为“
项和,则称该数列为“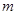 和数列”,若等差数列
和数列”,若等差数列 是一个“2012和数列”,且
是一个“2012和数列”,且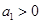 ,则其前
,则其前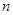 项和最大时
项和最大时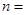 。
。
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(上海) 题型:解答题
若有穷数列 (
(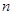 是正整数),满足
是正整数),满足 即
即
( 是正整数,且
是正整数,且 ),就称该数列为“对称数列”。
),就称该数列为“对称数列”。
(1)已知数列 是项数为7的对称数列,且
是项数为7的对称数列,且 成等差数列,
成等差数列, ,试写出
,试写出 的每一项
的每一项
(2)已知 是项数为
是项数为 的对称数列,且
的对称数列,且 构成首项为50,公差为
构成首项为50,公差为 的等差数列,数列
的等差数列,数列 的前
的前 项和为
项和为 ,则当
,则当 为何值时,
为何值时, 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数 ,试写出所有项数不超过
,试写出所有项数不超过 的对称数列,使得
的对称数列,使得 成为数列中的连续项;当
成为数列中的连续项;当 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com