
分析 利用特例判断①的正误;利用直线与平面垂直的判定定理以及性质定理判断②的正误;利用直接推理判断③的正误;利用特例判断④的正误;利用几何概型求解判断⑤的正误;
解答 解:①如图:(1)四面体满足AB⊥CD,但是AC⊥BD不成立;①不正确;
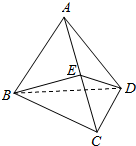
②如图:(2),AC=BC=AD=BD,去AB的中点E,连结EC,ED,可知AB⊥平面CDE,则AB⊥CD;②正确;
③点E,F分别在BC,BD上,且CD∥平面AEF,则EF∥CD,EF不一定是△BCD的中位线;所以③不正确;
④如图(4),若E是CD中点,则CD⊥平面ABE,显然不正确;
⑤在棱AB上任取一点P,使三棱锥P-BCD的体积与四面体ABCD的体积比大于$\frac{1}{3}$,则P到B的距离大于$\frac{1}{3}$,
两个棱锥的底面面积相同,所以所求的概率为$\frac{2}{3}$.正确.
故答案为:②⑤.
点评 本题考查命题的真假的判断与应用,棱锥的特征以及直线与平面垂直的判断与性质定理的应用,几何概型的求法,考查计算能力以及空间想象能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点.
如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AD∥BC,且AB=2BC=4,PA=AD=3,∠ABC=60°,E是BC的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AD∥BC,且AB=2BC=4,PA=AD=3,∠ABC=60°,E是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平面ABC⊥平面BCD,AB=BC=BD=2,∠ABC=∠DBC=$\frac{π}{3}$,E为棱AD的中点.
如图,平面ABC⊥平面BCD,AB=BC=BD=2,∠ABC=∠DBC=$\frac{π}{3}$,E为棱AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com