
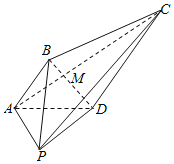
【题目】在四棱锥P–ABCD中,![]() ,
,![]() .
.
(1)设AC与BD相交于点M,![]() ,且
,且![]() 平面PCD,求实数m的值;
平面PCD,求实数m的值;
(2)若![]() ,
,![]() ,
,![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]()
(2)![]()
【解析】
(1)由AB∥CD,得到![]() ,由MN∥平面PCD,得MN∥PC,从而
,由MN∥平面PCD,得MN∥PC,从而![]() ,由此能实数m的值;
,由此能实数m的值;
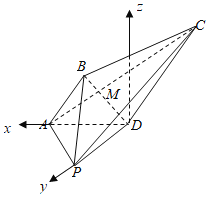
(2)由AB=AD,∠BAD=60°,知△ABD为等边三角形,推导出PD⊥DB,PD⊥AD,从而PD⊥平面ABCD,以D为坐标原点,![]() 的方向为x,y轴的正方向建立空间直角坐标系,由此能求出二面角B﹣PC﹣B的余弦值.
的方向为x,y轴的正方向建立空间直角坐标系,由此能求出二面角B﹣PC﹣B的余弦值.
解:(1)因为![]() ,所以
,所以![]() ,即
,即![]() .
.
因为![]() 平面PCD,
平面PCD,![]() 平面PAC,平面
平面PAC,平面![]() 平面
平面![]() ,
,
所以![]() .
.
所以![]() ,即
,即![]() .
.
(2)因为![]() ,
,![]() ,可知
,可知![]() 为等边三角形,
为等边三角形,
所以![]() ,又
,又![]() ,
,
故![]() ,所以
,所以![]() .
.
由已知![]() ,
,![]() ,所以
,所以![]() 平面ABCD,
平面ABCD,
如图,以D为坐标原点,![]() 的方向为x,y轴的正方向建立空间直角坐标系,
的方向为x,y轴的正方向建立空间直角坐标系,
设![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,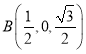 ,
,![]() ,
,![]() ,
,
则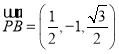 ,
,![]() ,
,![]()
设平面PBC的一个法向量为![]() ,则有
,则有
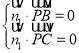 即
即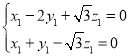 .
.
令![]() ,则
,则![]() ,即
,即![]() ,
,
设平面APC的一个法向量为![]() ,则有
,则有
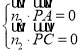 ,即
,即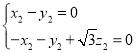
令![]() ,则
,则![]() ,即
,即![]() .
.
所以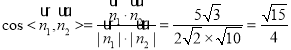
设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 是奇函数(其中
是奇函数(其中![]() )
)
(1)求实数m的值;
(2)已知关于x的方程![]() 在区间
在区间![]() 上有实数解,求实数k的取值范围;
上有实数解,求实数k的取值范围;
(3)当![]() 时,
时,![]() 的值域是
的值域是![]() ,求实数n与a的值.
,求实数n与a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax3+3x2+3x(a≠0).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间(1,2)是增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 其右顶点为
其右顶点为![]() ,下顶点为
,下顶点为![]() ,定点
,定点![]() ,
,![]() 的面积为
的面积为![]() 过点
过点![]() 作与
作与![]() 轴不重合的直线
轴不重合的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)试探究![]() 的横坐标的乘积是否为定值,说明理由.
的横坐标的乘积是否为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定函数![]() 和
和![]() ,令
,令![]() ,对以下三个论断:
,对以下三个论断:
(1)若![]() 和
和![]() 都是奇函数,则
都是奇函数,则![]() 也是奇函数;(2)若
也是奇函数;(2)若![]() 和
和![]() 都是非奇非偶函数,则
都是非奇非偶函数,则![]() 也是非奇非偶函数:(3)
也是非奇非偶函数:(3)![]() 和
和![]() 之一与
之一与![]() 有相同的奇偶性;其中正确论断的个数为( )
有相同的奇偶性;其中正确论断的个数为( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校兴趣小组在如图所示的矩形区域![]() 内举行机器人拦截挑战赛,在
内举行机器人拦截挑战赛,在![]() 处按
处按![]() 方向释放机器人甲,同时在
方向释放机器人甲,同时在![]() 处按某方向释放机器人乙,设机器人乙在
处按某方向释放机器人乙,设机器人乙在![]() 处成功拦截机器人甲.若点
处成功拦截机器人甲.若点![]() 在矩形区域
在矩形区域![]() 内(包含边界),则挑战成功,否则挑战失败.已知
内(包含边界),则挑战成功,否则挑战失败.已知![]() 米,
米,![]() 为
为![]() 中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记
中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记![]() 与
与![]() 的夹角为
的夹角为![]() .
.
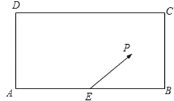
(1)若![]() ,
,![]() 足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到
足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到![]() );
);
(2)如何设计矩形区域![]() 的宽
的宽![]() 的长度,才能确保无论
的长度,才能确保无论![]() 的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域
的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域![]() 内成功拦截机器人甲?
内成功拦截机器人甲?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]()
(l)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 设
设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 |
|
社会人士 | 600人 |
|
|
(1)已知在全体样本中随机抽取![]() 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为![]() ,现用分层抽样的方法在所有参与调查的人中抽取
,现用分层抽样的方法在所有参与调查的人中抽取![]() 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取![]() 人,再平均分成两组进行深入交流,求第一组中在校学生人数
人,再平均分成两组进行深入交流,求第一组中在校学生人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com