
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
分析 由${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$,求出等比数列的前3项,由等比数列的性质得:${{a}_{2}}^{2}={a}_{1}{a}_{3}$,由此能求出实数a的值.
解答 解:∵等比数列{an}的前项和为Sn=2×(-1)n+a,n∈N*,
∴a1=S1=-2+a,
a2=S2-S1=(2+a)-(-2+a)=4,
${a}_{3}={S}_{3}-{S}_{2}^{\;}$=(-2+a)-(2+a)=-4,
由等比数列的性质得:${{a}_{2}}^{2}={a}_{1}{a}_{3}$,
∴42=(-2+a)•(-4),
解得a=-2.
故选:B.
点评 本题考查实数值的求法,是基础题,解题时要注意公式${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$和等比数列的性质的合理运用.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ( ) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{4}$) | D. | (0,$\frac{1}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
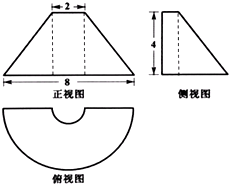 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )| A. | 12+$\frac{47π}{2}$ | B. | 12+23π | C. | 12+24π | D. | 12+$\frac{45}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{3}+2\sqrt{3}$ | B. | $\frac{16π}{3}+4\sqrt{3}$ | C. | $\frac{24π}{3}+2\sqrt{3}$ | D. | $\frac{24π}{3}+4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | a | 8 | 6 | 5 |
| A. | 7 | B. | 8.5 | C. | 9 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com