
A. | B. | C. | D. |
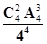 =
=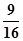 .
.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 满足
满足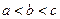 .
. 是从
是从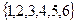 中任取的三个数,求
中任取的三个数,求 能构成三角形三边长的概率;
能构成三角形三边长的概率; 是从区间
是从区间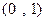 内任取的三个数,求
内任取的三个数,求 能构成三角形三边长的概率.
能构成三角形三边长的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
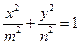
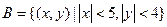 且焦点在X轴的椭圆的概率;
且焦点在X轴的椭圆的概率;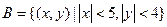 且焦点在X轴的椭圆的情况下,求离心率为
且焦点在X轴的椭圆的情况下,求离心率为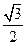
 的概率
的概率查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
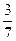 .现有甲、乙两人从袋中轮流摸取1球,取后不放回:甲先取,乙后取,然后甲再取……,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
.现有甲、乙两人从袋中轮流摸取1球,取后不放回:甲先取,乙后取,然后甲再取……,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 三次试验成功的概率是多少?
三次试验成功的概率是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
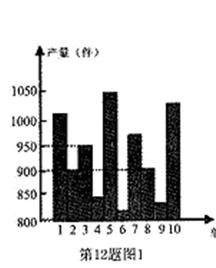
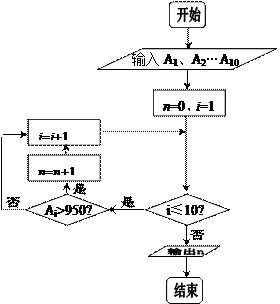 | |||
| |||
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
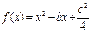
 别是先后抛掷一枚骰子得到的点数,求对任意x∈R,f(x)﹥0恒成立的概率。
别是先后抛掷一枚骰子得到的点数,求对任意x∈R,f(x)﹥0恒成立的概率。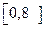 任取得一个数,c是从
任取得一个数,c是从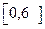 任取的一个数,求函数f(x)的图像与x轴有交点的概率。
任取的一个数,求函数f(x)的图像与x轴有交点的概率。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com