
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若不等式![]() 的解集包含[–1,1],求
的解集包含[–1,1],求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)分![]() ,
, ![]() ,
, ![]() 三种情况解不等式
三种情况解不等式![]() ;(2)
;(2)![]() 的解集包含
的解集包含![]() ,等价于当
,等价于当![]() 时
时![]() ,所以
,所以![]() 且
且![]() ,从而可得
,从而可得![]() .
.
试题解析:(1)当![]() 时,不等式
时,不等式![]() 等价于
等价于![]() .①
.①
当![]() 时,①式化为
时,①式化为![]() ,无解;
,无解;
当![]() 时,①式化为
时,①式化为![]() ,从而
,从而![]() ;
;
当![]() 时,①式化为
时,①式化为![]() ,从而
,从而![]() .
.
所以![]() 的解集为
的解集为![]() .
.
(2)当![]() 时,
时, ![]() .
.
所以![]() 的解集包含
的解集包含![]() ,等价于当
,等价于当![]() 时
时![]() .
.
又![]() 在
在![]() 的学科&网最小值必为
的学科&网最小值必为![]() 与
与![]() 之一,所以
之一,所以![]() 且
且![]() ,得
,得![]() .
.
所以![]() 的取值范围为
的取值范围为![]() .
.
点睛:形如![]() (或
(或![]() )型的不等式主要有两种解法:
)型的不等式主要有两种解法:
(1)分段讨论法:利用绝对值号内式子对应方程的根,将数轴分为![]() ,
, ![]() ,
, ![]() (此处设
(此处设![]() )三个部分,将每部分去掉绝对值号并分别列出对应的不等式求解,然后取各个不等式解集的并集.
)三个部分,将每部分去掉绝对值号并分别列出对应的不等式求解,然后取各个不等式解集的并集.
(2)图像法:作出函数![]() 和
和![]() 的图像,结合图像求解.
的图像,结合图像求解.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面ABCD为梯形,
的底面ABCD为梯形,![]() ,则在面PBC内
,则在面PBC内![]()
![]()

A. 一定存在与CD平行的直线
B. 一定存在与AD平行的直线
C. 一定存在与AD垂直的直线
D. 不存在与CD垂直的直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产![]() 、
、![]() 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于![]() 为正品,小于
为正品,小于![]() 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各![]() 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:
|
|
|
|
|
|
B |
|
|
|
|
|
由于表格被污损,数据![]() 、
、![]() 看不清,统计员只记得
看不清,统计员只记得![]() ,且
,且、
![]() 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(1)求表格中![]() 与
与![]() 的值;
的值;
(2)从被检测的![]() 件
件![]() 种元件中任取
种元件中任取![]() 件,求
件,求![]() 件都为正品的概率.
件都为正品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一条动直线3(m+1)x+(m-1)y-6m-2=0,
(1)求证:直线恒过定点,并求出定点P的坐标;
(2)若直线与x、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6,若存在,求出方程;若不存在,请说明理由.
(3)若直线与x、y轴的正半轴分别交于A,B两点,当![]() 取最小值时,求直线的方程.
取最小值时,求直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
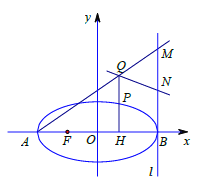
【题目】如图,已知椭圆![]() 的长轴长为
的长轴长为![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴垂直,椭圆的离心率
轴垂直,椭圆的离心率![]() ,
, ![]() 为椭圆的左焦点,且
为椭圆的左焦点,且![]() .
.
(Ⅰ)求此椭圆的方程;
(Ⅱ)设![]() 是此椭圆上异于
是此椭圆上异于![]() 的任意一点,
的任意一点, ![]() 轴,
轴, ![]() 为垂足,延长
为垂足,延长![]() 到点
到点![]() 使得
使得![]() .连接
.连接![]() 并延长,交直线
并延长,交直线![]() 于点
于点![]() 为
为![]() 的中点,判定直线
的中点,判定直线![]() 与以
与以![]() 为直径的圆
为直径的圆![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数![]()
![]() 的部分图象,M,N是它与x轴的两个不同交点,D是M,N之间的最高点且横坐标为
的部分图象,M,N是它与x轴的两个不同交点,D是M,N之间的最高点且横坐标为![]() ,点
,点![]() 是线段DM的中点.
是线段DM的中点.

(1)求函数![]() 的解析式及
的解析式及![]() 上的单调增区间;
上的单调增区间;
(2)若![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次考试后,对全班同学的数学成绩进行整理,得到表:
分数段 |
|
|
|
|
人数 | 5 | 15 | 20 | 10 |
将以上数据绘制成频率分布直方图后,可估计出本次考试成绩的中位数是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意实数a,b,c,给出下列命题:
①“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
②“![]() 是无理数”是“a是无理数”的充要条件;
是无理数”是“a是无理数”的充要条件;
③“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
④“![]() ”是“
”是“![]() ”的必要不充分条件,
”的必要不充分条件,
其中真命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com