
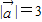 ,
,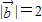 ,且
,且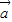 与
与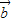 的夹角为60°,则
的夹角为60°,则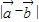 = .
= .  王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| π |
| 6 |
| α-β |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| π |
| 6 |
| π |
| 6 |
| b |
| π |
| 6 |
| π |
| 6 |
| b |
| a |
| b |
| a |
| b |
| m |
| t |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:022
(1)
已知 ,
, ,
, 是三条直线,且
是三条直线,且 ∥
∥ ,
, 与
与 的夹角为
的夹角为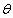 ,那么
,那么 与
与 夹角为______;
夹角为______;
(2)
如下图, 是长方体的一条棱,这个长方体中与
是长方体的一条棱,这个长方体中与 垂直的棱共______条;
垂直的棱共______条;

(3)
如果 ,
, 是异面直线,直线
是异面直线,直线 与
与 ,
,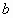 都相交,那么这三条直线中的两条所确定的平面共有_______个;
都相交,那么这三条直线中的两条所确定的平面共有_______个;
(4)
若一条直线与两个平行平面中的一个平面平行,则这条直线与另一个平面的位置关系是______;(5)
已知两条相交直线 ,
, ,
, ∥平面
∥平面 ,则
,则 与
与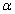 的位置关系是______;
的位置关系是______;
(6)设直线
 ,
, 分别是长方体相邻两个面的对角线所在的直线,则
分别是长方体相邻两个面的对角线所在的直线,则 与
与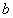 的位置关系是______.
的位置关系是______.查看答案和解析>>
科目:高中数学 来源: 题型:
(08年重庆一中一模理)(本小题满分12分,其中⑴小问6分,⑵小问6分)过点![]() 作倾斜角为
作倾斜角为![]() 的直线,交抛物线
的直线,交抛物线![]() :
:![]() 于
于![]() 两点,且
两点,且![]() 成等比数列。⑴求
成等比数列。⑴求![]() 的方程;⑵过点
的方程;⑵过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点。设
两点。设![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,求证:
,求证:![]() 。
。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com