
【题目】在四面体![]() 中,已知
中,已知![]() ,
,![]() .
.
(1)当四面体体积最大时,求![]() 的值;
的值;
(2)当![]() 时,设四面体
时,设四面体![]() 的外接球球心为
的外接球球心为![]() ,求
,求![]() 和平面
和平面![]() 所成夹角的正弦值.
所成夹角的正弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
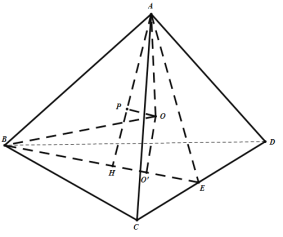
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,由题意可知当
,由题意可知当![]() 平面
平面![]() 时,四面体的面积最大,求出此时的
时,四面体的面积最大,求出此时的![]() 的值即可得解;
的值即可得解;
(2)在线段![]() 上取
上取![]() ,使
,使![]() ,
,![]() 为
为![]() 的内心,过
的内心,过![]() 作
作![]() 平面
平面![]() ,则球心在直线
,则球心在直线![]() 上,设
上,设![]() ,球的半径为
,球的半径为![]() ,由勾股定理求得
,由勾股定理求得![]() 后,由
后,由![]() 即可得解.
即可得解.
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,
,
由![]() 可得
可得![]() ,
,![]() ,
,![]() ,
,
由![]() 可得
可得![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
即![]() 即为四面体的高,由
即为四面体的高,由![]() ,可知当
,可知当![]() 平面
平面![]() 四面体面积最大,
四面体面积最大,
此时![]() 即
即![]() 的值为
的值为![]() ;
;
(2)当![]() 时,
时,![]() ,则
,则![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,![]() ,
,
在线段![]() 上取
上取![]() ,使
,使![]() ,易知
,易知![]() 为
为![]() 的内心,
的内心,![]() ,
,
过![]() 作
作![]() 平面
平面![]() ,则球心在直线
,则球心在直线![]() 上,
上,
球心为![]() ,过点
,过点![]() 作
作![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() ,
,
设![]() ,球的半径为
,球的半径为![]() ,则
,则![]() ,
,
则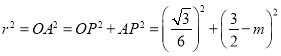 ,
,
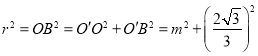 ,
,
所以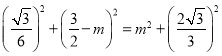 ,解得
,解得![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设![]() 和平面
和平面![]() 所成夹角为
所成夹角为![]() ,
,
由![]() 平面
平面![]() 可知
可知![]() ,
,
所以![]() 和平面
和平面![]() 所成夹角的正弦值为
所成夹角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),
为参数),![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)化![]() 、
、![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,曲线
,曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,曲线
,曲线![]() 上的点
上的点![]() 对应的参数
对应的参数![]() ,求
,求![]() 的中点
的中点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 有两个不同的零点
有两个不同的零点![]() .
.
(ⅰ)求实数![]() 的取值范围;
的取值范围;
(ⅱ)求证:![]() .(其中
.(其中![]() 为
为![]() 的极小值点)
的极小值点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
的棱长为1,P是空间中任意一点,下列正确命题的个数是( )

①若P为棱![]() 中点,则异面直线AP与CD所成角的正切值为
中点,则异面直线AP与CD所成角的正切值为![]() ;
;
②若P在线段![]() 上运动,则
上运动,则![]() 的最小值为
的最小值为![]() ;
;
③若P在半圆弧CD上运动,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 外接球的表面积为
外接球的表面积为![]() ;
;
④若过点P的平面![]() 与正方体每条棱所成角相等,则
与正方体每条棱所成角相等,则![]() 截此正方体所得截面面积的最大值为
截此正方体所得截面面积的最大值为![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中点(如图1),将
是EA的中点(如图1),将![]() 沿CD折起到图2中
沿CD折起到图2中![]() 的位置,得到四棱锥是
的位置,得到四棱锥是![]() .
.

(1)求证:![]() 平面PDA;
平面PDA;
(2)若PD与平面ABCD所成的角为![]() .且
.且![]() 为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了政府对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房的心理预期调研,用简单随机抽样的方法抽取110人进行统计,得到如下列联表:
买房 | 不买房 | 纠结 | |
城市人 | 5 | 15 | |
农村人 | 20 | 10 |
已知样本中城市人数与农村人数之比是3:8.
![]() 分别求样本中城市人中的不买房人数和农村人中的纠结人数;
分别求样本中城市人中的不买房人数和农村人中的纠结人数;
![]() 用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关?
用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关?
参考公式:![]() .
.
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() (
(![]() 为常数)对于任意的
为常数)对于任意的![]() 恒成立.
恒成立.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,关于
,关于![]() 的不等式
的不等式![]() 有且仅有两个不同的整数解,求
有且仅有两个不同的整数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上运动,
轴上运动,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,若直线
,若直线![]() ,
,![]() 的斜率之和为2,直线
的斜率之和为2,直线![]() 是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为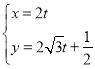 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设动点![]() 在圆
在圆![]() 上,动线段
上,动线段![]() 的中点
的中点![]() 的轨迹为
的轨迹为![]() ,
,![]() 与直线
与直线![]() 交点为
交点为![]() ,且直角坐标系中,
,且直角坐标系中,![]() 点的横坐标大于
点的横坐标大于![]() 点的横坐标,求点
点的横坐标,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com