
°æƒø°øº◊°¢““¡ΩŒª—ß…˙≤Œº” ˝—ßæ∫»¸≈ý—µ£¨‘⁄≈ý—µ∆⁄º‰£¨À˚√«≤Œº”µƒ5¥Œ‘§»¸≥…º®º«¬º»Áœ¬£∫
º◊ | 82 | 82 | 79 | 95 | 87 |
““ | 95 | 75 | 80 | 90 | 85 |
£®1£©«Î”√æ•“∂Õº±Ì æ’‚¡Ω◊È ˝æð£ª
£®2£©¥”º◊°¢““¡Ω»Àµƒ≥…º®÷–∏˜Àʪ˙≥È»°“ª∏ˆ£¨«Ûº◊µƒ≥…º®±»““∏þµƒ∏≈¬ £ª
£®3£©œ÷“™¥”÷–—°≈…“ª»À≤Œº”9‘¬∑𵃻´π˙ ˝—ß¡™»¸£¨¥”Õ≥º∆—ßµƒΩ«∂»øº¬«£¨ƒ„»œŒ™—°≈…ƒƒŒª—ß…˙≤Œº”∫œ £ø«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø
£®1£©Ω‚£∫◊˜≥ˆæ•“∂Õº»Áœ¬Õº
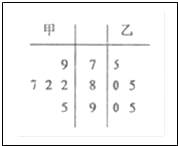
£®2£©Ω‚£∫º«º◊±ª≥ÈµΩµƒ≥…º®Œ™x£¨““±ª≥ȵΩ≥…º®Œ™y£¨”√ ˝∂‘£®x£¨y£©±Ì æª˘±æ ¬º˛£∫
£®82£¨95£©£¨£®82£¨75£©£¨£®82£¨80£©£¨£®82£¨90£©£¨£®82£¨85£©£¨
£®82£¨95£©£¨£®82£¨75£©£¨£®82£¨80£©£¨£®82£¨90£©£¨£®82£¨85£©£¨
£®79£¨95£©£¨£®79£¨75£©£¨£®79£¨80£©£¨£®79£¨90£©£¨£®79£¨85£©£¨
£®95£¨95£©£¨£®95£¨75£©£¨£®95£¨80£©£¨£®95£¨90£©£¨£®95£¨85£©£¨
£®87£¨95£©£¨£®87£¨75£©£¨£®87£¨80£©£¨£®87£¨90£©£¨£®87£¨85£©£¨
ª˘±æ ¬º˛◊Ð ˝n=25
º«°∞º◊µƒ≥…º®±»““∏þ°±Œ™ ¬º˛A£¨ ¬º˛A∞¸∫¨µƒª˘±æ ¬º˛£∫
£®82£¨75£©£¨£®82£¨80£©£¨£®82£¨75£©£¨£®82£¨80£©£¨£®79£¨75£©£¨£®95£¨75£©£¨
£®95£¨80£©£¨£®95£¨90£©£¨£®95£¨85£©£¨£®87£¨75£©£¨£®87£¨80£©£¨£®87£¨85£©£¨
¬º˛A∞¸∫¨µƒª˘±æ ¬º˛ ˝m=12
À˘“‘ ![]()
£®3£©Ω‚£∫≈…º◊≤Œ»¸±»Ωœ∫œ £¨¿Ì”…»Áœ¬£∫ ![]() =
= ![]() £®70°¡1+80°¡3+90°¡1+9+2+2+7+5£©=85£¨
£®70°¡1+80°¡3+90°¡1+9+2+2+7+5£©=85£¨
![]() =
= ![]() £®70°¡1+80°¡2+90°¡2+5+0+5+0+5£©=85
£®70°¡1+80°¡2+90°¡2+5+0+5+0+5£©=85
![]()
![]()
°þ ![]() =
= ![]() £¨Sº◊2£ºS““2°ýº◊µƒ≥…º®ΩœŒ»∂®£¨≈…º◊≤Œ»¸±»Ωœ∫œ
£¨Sº◊2£ºS““2°ýº◊µƒ≥…º®ΩœŒ»∂®£¨≈…º◊≤Œ»¸±»Ωœ∫œ
°æΩ‚Œˆ°ø£®1£©”√æ•“∂Õº±Ì æ¡Ω◊È ˝æ𣨠◊œ»“™œ»»∑∂®°∞æ•°±÷µ£¨‘ŸΩ´ ˝æð∞¥°∞æ•°±÷µ∑÷◊È∑÷¿ý±Ì æ‘⁄°∞“∂°±µƒŒª÷√£Æ£®2£©“™¥”º◊°¢““¡Ω»Àµƒ≥…º®÷–∏˜Àʪ˙≥È»°“ª∏ˆ£¨«Ûº◊µƒ≥…º®±»““∏þµƒ∏≈¬ £¨ ◊œ»“™º∆À„°∞“™¥”º◊°¢““¡Ω»Àµƒ≥…º®÷–∏˜Àʪ˙≥È»°“ª∏ˆ°±µƒ ¬º˛∏ˆ ˝£¨‘Ÿº∆À„°∞º◊µƒ≥…º®±»““∏þ°±µƒ ¬º˛∏ˆ ˝£¨¥˙»Îπ≈µ‰∏≈–Õπ´ Ωº¥ø…«ÛΩ‚£Æ£®3£©—°≈…—ß…˙≤Œº”¥Û–Õ±»»¸£¨ «“™—∞’“≥…º®∑¢ª”±»ΩœŒ»∂®µƒ”≈–„—ß…˙£¨À˘“‘“™œ»∑÷Œˆ¡Ω√˚—ß…˙µƒ∆Ωæ˘≥…º®£¨»Ù∆Ωæ˘≥…º®œýµ»£¨‘Ÿ”…æ•“∂Õº∑÷Œˆ≥ˆ≥…º®œý±»Œ»∂®µƒ—ß…˙≤Œº”£Æ
°æøºµ„æ´Œˆ°ø±æÂ÷˜“™øº≤È¡Àæ•“∂Õº∫Õº´≤Ó°¢∑Ω≤ӔαÍ◊º≤Óµƒœýπÿ÷™ ∂µ„£¨–Ë“™’∆Œ’æ•“∂Õº”÷≥∆°∞÷¶“∂Õº°±£¨À¸µƒÀº¬∑ «Ω´ ˝◊È÷–µƒ ˝∞¥Œª ˝Ω¯––±»Ωœ£¨Ω´ ˝µƒ¥Û–°ª˘±æ≤ª±‰ªÚ±‰ªØ≤ª¥ÛµƒŒª◊˜Œ™“ª∏ˆ÷˜∏…£®æ•£©£¨Ω´±‰ªØ¥ÛµƒŒªµƒ ˝◊˜Œ™∑÷÷¶£®“∂£©£¨¡–‘⁄÷˜∏…µƒ∫Û√Ê£¨’‚—˘æÕø…“‘«Â≥˛µÿø¥µΩ√ø∏ˆ÷˜∏…∫Û√ʵƒº∏∏ˆ ˝£¨√ø∏ˆ ˝æþà«∂ý…Ÿ£ª±Í◊º≤Ó∫Õ∑Ω≤Ó‘Ω¥Û£¨ ˝æ𵃿΅¢≥Ã∂»‘Ω¥Û£ª±Í◊º≤Ó∫Õ∑Ω≥ÃŒ™0 ±£¨—˘±æ∏˜ ˝æð»´œýµ»£¨ ˝æð√ª”–¿Î…¢–‘£ª∑Ω≤ӔΑ≠ º ˝æ𵕌ª≤ªÕ¨£¨Ω‚æˆ µº Œ  ±£¨∂ý≤…”√±Í◊º≤Ó≤≈ƒÐ’˝»∑Ω‚¥¥À£Æ


 ΩÚ«≈ΩÔ˝º∆À„–°◊¥‘™œµ¡–¥∞∏
ΩÚ«≈ΩÔ˝º∆À„–°◊¥‘™œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£∏þ∂˛ƒÍº∂—ß…˙ª·”–¿Ìø∆…˙4√˚£¨∆‰÷–3√˚ƒ–Õ¨—ߣªŒƒø∆…˙3√˚£¨∆‰÷–”–1√˚ƒ–Õ¨—ß.¥”’‚7√˚≥…‘±÷–Àʪ˙≥È4»À≤Œº”∏þ÷– æ∑∂–£—È ’ªÓ∂ØŒ æ̵˜≤È.
£®¢Ò£©…Ë![]() Œ™ ¬º˛°∞—°≥ˆµƒ4»À÷–º»”–Œƒø∆…˙”÷”–¿Ìø∆…˙°±£¨«Û ¬º˛
Œ™ ¬º˛°∞—°≥ˆµƒ4»À÷–º»”–Œƒø∆…˙”÷”–¿Ìø∆…˙°±£¨«Û ¬º˛![]() µƒ∏≈¬ £ª
µƒ∏≈¬ £ª
£®¢Ú£©…Ë![]() Œ™—°≥ˆµƒ4»À÷–ƒ–…˙»À ˝”Î≈Æ…˙»À ˝≤Óµƒæ¯∂‘÷µ£¨«ÛÀʪ˙±‰¡ø
Œ™—°≥ˆµƒ4»À÷–ƒ–…˙»À ˝”Î≈Æ…˙»À ˝≤Óµƒæ¯∂‘÷µ£¨«ÛÀʪ˙±‰¡ø![]() µƒ∑÷≤º¡–∫Õ ˝—ß∆⁄Õ˚.
µƒ∑÷≤º¡–∫Õ ˝—ß∆⁄Õ˚.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨∆Ω√ÊABCD°Õ∆Ω√ÊADEF£¨Àƒ±þ–ŒABCDŒ™¡‚–Œ£¨Àƒ±þ–ŒADEFŒ™æÿ–Œ£¨M°¢N∑÷± «EF°¢BCµƒ÷–µ„£¨AB=2AF=2£¨°œCBA=60°„£Æ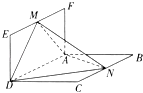
£®1£©«Û÷§£∫AN°ÕDM£ª
£®2£©«Û÷±œþMN”Î∆Ω√ÊADEFÀ˘≥…µƒΩ«µƒ’˝«–÷µ£ª
£®3£©«Û»˝¿‚◊∂D©ÅMANµƒÃª˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄÷±Ω«◊¯±Íœµ ![]() ÷–£¨“‘‘≠µ„
÷–£¨“‘‘≠µ„ ![]() Œ™º´µ„£¨“‘
Œ™º´µ„£¨“‘ ![]() ÷·’˝∞Î÷·Œ™º´÷·£¨Ω®¡¢º´◊¯±Íœµ£¨«˙œþ
÷·’˝∞Î÷·Œ™º´÷·£¨Ω®¡¢º´◊¯±Íœµ£¨«˙œþ ![]() µƒº´◊¯±Í∑Ω≥ÃŒ™
µƒº´◊¯±Í∑Ω≥ÃŒ™ ![]() £¨«˙œþ
£¨«˙œþ ![]() µƒ≤Œ ˝∑Ω≥ÃŒ™
µƒ≤Œ ˝∑Ω≥ÃŒ™ ![]() £Æ
£Æ
£®1£©«Û«˙œþ ![]() µƒ÷±Ω«◊¯±Í∑Ω≥ÔΫ˙œþ
µƒ÷±Ω«◊¯±Í∑Ω≥ÔΫ˙œþ ![]() µƒ∆’Õ®∑Ω≥ãª
µƒ∆’Õ®∑Ω≥ãª
£®2£© ‘≈–∂œ«˙œþ ![]() ”Î
”Î ![]() «∑ҥʑ⁄¡Ω∏ˆΩªµ„£ø»Ù¥Ê‘⁄£¨«Û≥ˆ¡ΩΩªµ„º‰µƒæý¿Î£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
«∑ҥʑ⁄¡Ω∏ˆΩªµ„£ø»Ù¥Ê‘⁄£¨«Û≥ˆ¡ΩΩªµ„º‰µƒæý¿Î£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø—°–Þ4°™4£∫◊¯±Íœµ”Î≤Œ ˝∑Ω≥Ã
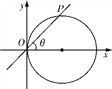
(¢Ò)»ÁÕº£¨“‘π˝‘≠µ„µƒ÷±œþµƒ«„–±Ω«¶»Œ™≤Œ ˝£¨«Û‘≤x2£´y2£≠x£Ω0µƒ≤Œ ˝∑Ω≥ãª
(¢Ú)‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨“—÷™÷±œþlµƒ≤Œ ˝∑Ω≥ÃŒ™![]() (sŒ™≤Œ ˝)£¨«˙œþCµƒ≤Œ ˝∑Ω≥ÃŒ™
(sŒ™≤Œ ˝)£¨«˙œþCµƒ≤Œ ˝∑Ω≥ÃŒ™![]() (tŒ™≤Œ ˝)£¨»Ùl”ÎCœýΩª”⁄A£¨B¡Ωµ„£¨«ÛABµƒ≥§£Æ
(tŒ™≤Œ ˝)£¨»Ùl”ÎCœýΩª”⁄A£¨B¡Ωµ„£¨«ÛABµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄÷±Ω«◊¯±Íœµ ![]() ÷–£¨«˙œþ
÷–£¨«˙œþ ![]() µƒ≤Œ ˝∑Ω≥ÃŒ™
µƒ≤Œ ˝∑Ω≥ÃŒ™ 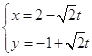 £®
£® ![]() Œ™≤Œ ˝£©£¨“‘‘≠µ„
Œ™≤Œ ˝£©£¨“‘‘≠µ„ ![]() Œ™º´µ„£¨“‘
Œ™º´µ„£¨“‘ ![]() ÷·’˝∞Î÷·Œ™º´÷·£¨Ω®¡¢º´◊¯±Íœµ£¨«˙œþ
÷·’˝∞Î÷·Œ™º´÷·£¨Ω®¡¢º´◊¯±Íœµ£¨«˙œþ ![]() µƒº´◊¯±Í∑Ω≥ÃŒ™
µƒº´◊¯±Í∑Ω≥ÃŒ™ ![]() £Æ
£Æ
£®1£©«Û«˙œþ ![]() µƒ∆’Õ®∑Ω≥ÔΫ˙œþ
µƒ∆’Õ®∑Ω≥ÔΫ˙œþ ![]() µƒ÷±Ω«◊¯±Í∑Ω≥ãª
µƒ÷±Ω«◊¯±Í∑Ω≥ãª
£®2£© ‘≈–∂œ«˙œþ ![]() ”Î
”Î ![]() «∑ҥʑ⁄¡Ω∏ˆΩªµ„£¨»Ù¥Ê‘⁄£¨«Û≥ˆ¡ΩΩªµ„º‰µƒæý¿Î£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
«∑ҥʑ⁄¡Ω∏ˆΩªµ„£¨»Ù¥Ê‘⁄£¨«Û≥ˆ¡ΩΩªµ„º‰µƒæý¿Î£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™![]() £¨Õ÷‘≤
£¨Õ÷‘≤![]() ∫Õ≈◊ŒÔœþ
∫Õ≈◊ŒÔœþ![]() Ωª”⁄
Ωª”⁄![]() ¡Ωµ„£¨«“÷±œþ
¡Ωµ„£¨«“÷±œþ![]() «°∫√Õ®π˝Õ÷‘≤
«°∫√Õ®π˝Õ÷‘≤![]() µƒ”“Ωπµ„
µƒ”“Ωπµ„![]() £¨
£¨
£®1£©«ÛÕ÷‘≤![]() µƒ±Í◊º∑Ω≥ãª
µƒ±Í◊º∑Ω≥ãª
£®2£©æ≠π˝![]() µƒ÷±œþ
µƒ÷±œþ![]() ∫ÕÕ÷‘≤
∫ÕÕ÷‘≤![]() Ωª”⁄
Ωª”⁄![]() ¡Ωµ„,Ωª≈◊ŒÔœþ”⁄
¡Ωµ„,Ωª≈◊ŒÔœþ”⁄![]() ¡Ωµ„£¨
¡Ωµ„£¨ ![]() «≈◊ŒÔœþµƒΩ𵄣¨ «∑ҥʑ⁄÷±œþ
«≈◊ŒÔœþµƒΩ𵄣¨ «∑ҥʑ⁄÷±œþ![]() £¨ πµ√
£¨ πµ√![]() ,»Ù¥Ê‘⁄£¨«Û≥ˆ÷±œþ
,»Ù¥Ê‘⁄£¨«Û≥ˆ÷±œþ![]() µƒ∑Ω≥㨻Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…°£
µƒ∑Ω≥㨻Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™![]() £¨Àƒ∏ˆ∂•µ„ππ≥…µƒ¡‚–Œµƒ√ʪ˝ «4£¨‘≤
£¨Àƒ∏ˆ∂•µ„ππ≥…µƒ¡‚–Œµƒ√ʪ˝ «4£¨‘≤![]() π˝Õ÷‘≤
π˝Õ÷‘≤![]() µƒ…œ∂•µ„
µƒ…œ∂•µ„![]() ◊˜‘≤
◊˜‘≤![]() µƒ¡ΩÃı«–œþ∑÷±”ÎÕ÷‘≤
µƒ¡ΩÃı«–œþ∑÷±”ÎÕ÷‘≤![]() œýΩª”⁄
œýΩª”⁄![]() ¡Ωµ„£®≤ªÕ¨”⁄µ„
¡Ωµ„£®≤ªÕ¨”⁄µ„![]() £©£¨÷±œþ
£©£¨÷±œþ![]() µƒ–±¬ ∑÷±Œ™
µƒ–±¬ ∑÷±Œ™![]() .
.
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©µ±![]() ±‰ªØ ±£¨¢Ÿ«Û
±‰ªØ ±£¨¢Ÿ«Û![]() µƒ÷µ£ª¢⁄ ‘Œ ÷±œþ
µƒ÷µ£ª¢⁄ ‘Œ ÷±œþ![]() «∑Òπ˝ƒ≥∏ˆ∂®µ„£ø»Ù «£¨«Û≥ˆ∏√∂®µ„£ª»Ù≤ª «£¨«ÎÀµ√˜¿Ì”….
«∑Òπ˝ƒ≥∏ˆ∂®µ„£ø»Ù «£¨«Û≥ˆ∏√∂®µ„£ª»Ù≤ª «£¨«ÎÀµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™œÚ¡ø![]() £¨
£¨ ![]() £¨∫Ø ˝
£¨∫Ø ˝![]() £¨∫Ø ˝
£¨∫Ø ˝![]() ‘⁄
‘⁄![]() ÷·…œµƒΩÿæýŒ“
÷·…œµƒΩÿæýŒ“![]() £¨”Î
£¨”Î![]() ÷·◊ÓΩ¸µƒ◊Ó∏þµ„µƒ◊¯±Í «
÷·◊ÓΩ¸µƒ◊Ó∏þµ„µƒ◊¯±Í «![]() £Æ
£Æ
£®¢Ò£©«Û∫Ø ˝![]() µƒΩ‚Œˆ Ω£ª
µƒΩ‚Œˆ Ω£ª
£®¢Ú£©Ω´∫Ø ˝![]() µƒÕºœÛœÚ◊Û∆Ω“∆
µƒÕºœÛœÚ◊Û∆Ω“∆![]() £®
£®![]() £©∏ˆµ•Œª£¨‘ŸΩ´ÕºœÛ…œ∏˜µ„µƒ◊ð◊¯±Í≤ª±‰£¨∫·◊¯±Í…Ï≥§µΩ‘≠¿¥µƒ2±∂£¨µ√µΩ∫Ø ˝
£©∏ˆµ•Œª£¨‘ŸΩ´ÕºœÛ…œ∏˜µ„µƒ◊ð◊¯±Í≤ª±‰£¨∫·◊¯±Í…Ï≥§µΩ‘≠¿¥µƒ2±∂£¨µ√µΩ∫Ø ˝![]() µƒÕºœÛ£¨«Û
µƒÕºœÛ£¨«Û![]() µƒ◊Ó–°÷µ£Æ
µƒ◊Ó–°÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com