
分析 (1)根据向量的坐标运算和向量的数量积和二倍角公式化简即可,并根据三角函数的性质即可求出单调区间,
(2)利用五点作图法,即可得到函数的图象.
解答 解:$\overrightarrow m=(\sqrt{3}sin\frac{x}{2},1),\overrightarrow n=(cos\frac{x}{2},{cos^2}\frac{x}{2})$
(1)$f(x)=2\overrightarrow m•\overrightarrow n-1$=$2(\sqrt{3}sin\frac{x}{2}cos\frac{x}{2}+{cos^2}\frac{x}{2})-1=\sqrt{3}sinx+cosx=2sin(x+\frac{π}{6})$,
由2kπ-$\frac{π}{2}$≤x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,解得2kπ-$\frac{2}{3}π$≤x≤2kπ+$\frac{1}{3}π$,k∈Z,
∴f(x)的单调递增区间为[2kπ-$\frac{2}{3}π$,2kπ+$\frac{1}{3}π$],k∈Z.
(2)列表如下:
| x | 0 | $\frac{π}{3}$ | $\frac{5}{6}$π | $\frac{4}{3}$π | $\frac{11}{6}$π | 2π |
| x+$\frac{π}{6}$ | $\frac{π}{6}$ | $\frac{π}{2}$ | π | $\frac{3}{2}$π | 2π | $\frac{13}{6}$π |
| y | 1 | 2 | 0 | -2 | 0 | 1 |
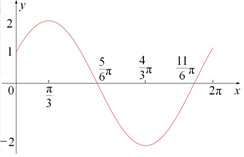
点评 本题主要考查了正弦函数的单调性,和两角和公式,二倍角公式的运用.三角函数的基本公式较多,注意多积累.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25π | B. | 200π | C. | 100π | D. | 50π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q为真 | B. | p∧q为真 | C. | p∨q为假 | D. | q为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{2}$ | B. | $\frac{21}{2}$ | C. | $\frac{21}{55}$ | D. | $\frac{23}{66}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com