
【题目】以下问题最终结果用数字表示
(1)由0、1、2、3、4可以组成多少个无重复数字的五位偶数?
(2)由1、2、3、4、5组成多少个无重复数字且2、3不相邻的五位数?
(3)由1、2、3、4、5组成多少个无重复数字且数字1,2,3必须按由大到小顺序排列的五位数?
【答案】(1)60 (2)72 (3)20
【解析】
(1)五位偶数,要求末位必须是0,2,4,分类求出满足条件的结果。
(2)可以求出一共能组成多少个五位数,然后再求出2、3相邻的五位数的个数,两数相减。
(3)确定数字4,5的排法,然后数字1,2,3按照3,2,1的顺序插入。
(1)偶数末位必须为0,2,4对此进行以下分类:
当末位是0时,剩下1,2,3,4进行全排列,![]() =24
=24
当末位是2时,注意0不能排在首位,首位从1,3,4选出有![]() 种方法排在首位,剩下的三个数可以进行全排列有
种方法排在首位,剩下的三个数可以进行全排列有![]() 种排法,所以当末位数字是2时有
种排法,所以当末位数字是2时有![]() =18个数。
=18个数。
同理当末位数字是4时也有18个数,
所以由0、1、2、3、4可以组成无重复数字的五位偶数有24+18+18=60个.
(2)由1、2、3、4、5组成五位数一共有![]() 个。
个。
第一步,把2.3捆定,有![]() 种排法;
种排法;
第二步,捆定的2,3与1,4,5一起全排列,共有![]() 个数,
个数,
根据分步计数原理,2,3相邻的五位数共有![]()
![]() =48个数,
=48个数,
因此由1、2、3、4、5组成无重复数字且2、3不相邻的五位数共有
![]() 个数。
个数。
(3)把五位数每个数位看成五个空,数字4,5共有![]() 个,
个,
然后把数字1,2,3按照3,2,1的顺序插入,只有一种方式,
根据分步计数原理,可知
由1、2、3、4、5组成无重复数字且数字1,2,3必须按由大到小顺序排列的五位数
为![]() 个。
个。


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() .
.
(1)若直线![]() 与直线
与直线![]() 平行,求实数
平行,求实数![]() 的值;
的值;
(2)若![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上,已知
上,已知![]() 的中点在
的中点在![]() 轴上,求点
轴上,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据两直线平行,对应方向向量共线,列方程即可求出![]() 的值;(2)根据
的值;(2)根据![]() 时,直线
时,直线![]() 的方程设出点
的方程设出点![]() 的坐标,由此求出
的坐标,由此求出![]() 的中点坐标,再由中点在
的中点坐标,再由中点在![]() 轴上求出点
轴上求出点![]() 的坐标.
的坐标.
试题解析:(1)∵直线![]() 与直线
与直线![]() 平行,
平行,
∴![]() ,
,
∴![]() ,经检验知,满足题意.
,经检验知,满足题意.
(2)由题意可知: ![]() ,
,
设![]() ,则
,则![]() 的中点为
的中点为![]() ,
,
∵![]() 的中点在
的中点在![]() 轴上,∴
轴上,∴![]() ,
,
∴![]() .
.
【题型】解答题
【结束】
16
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,前10万元按销售利润的15%进行奖励,若超出部分为t万元,则超出部分按![]() 进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出奖金y关于销售利润x的关系式;
(2)如果业务员小王获得3.5万元的奖金,那么他的销售利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
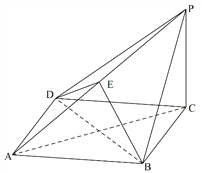
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,平面
为菱形,平面![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求证:
,求证: ![]() ;
;
(Ⅲ)是否存在点![]() ,使得四面体
,使得四面体![]() 的体积等于四面体
的体积等于四面体![]() 的
的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:(x+1)2+(y-3)2=9和圆C2:x2+y2-4x+2y-11=0.
(1)求两圆公共弦所在直线的方程;
(2)求直线过点C(3,-5),且与公共弦垂直的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() 具有性质
具有性质![]() :对任意的
:对任意的![]()
![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(Ⅱ)求证![]() ;
;
(Ⅲ)若![]() ,求数集
,求数集![]() 中所有元素的和的最小值.
中所有元素的和的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com