
【题目】某小区所有263户家庭人口数分组表示如下:
家庭人口数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
家庭数 | 20 | 29 | 48 | 50 | 46 | 36 | 19 | 8 | 4 | 3 |
(1)若将上述家庭人口数的263个数据分布记作![]() ,平均值记作
,平均值记作![]() ,写出人口数方差的计算公式(只要计算公式,不必计算结果);
,写出人口数方差的计算公式(只要计算公式,不必计算结果);
(2)写出他们家庭人口数的中位数(直接给出结果即可);
(3)计算家庭人口数的平均数与标准差.(写出公式,再利用计算器计算,精确到0.01)
科目:高中数学 来源: 题型:
【题目】某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润y1与投资金额x的函数关系为y1=18-![]() ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2=![]() (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).
(1)该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出定义域;
(2)在(1)的条件下,试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率为
的离心率为![]() ,左焦点为
,左焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围;
的取值范围;
(3)在![]() 轴上,是否存在定点
轴上,是否存在定点![]() ,使
,使![]() 恒为定值?若存在,求出
恒为定值?若存在,求出![]() 点的坐标和这个定值;若不存在,说明理由.
点的坐标和这个定值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,离心率为
,离心率为![]() .已知
.已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点, ![]() 到抛物线的准线
到抛物线的准线![]() 的距离为
的距离为![]() .
.
(I)求椭圆的方程和抛物线的方程;
(II)设![]() 上两点
上两点![]() ,
, ![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与椭圆相交于点
与椭圆相交于点![]() (
(![]() 异于点
异于点![]() ),直线
),直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形![]() 中,
中,![]() 、
、![]() 分
分![]() 、
、![]() 所成的比为
所成的比为![]() ,即
,即![]() ,则有:
,则有:![]() .
.

(1)拓展到空间,写出空间四边形![]() 类似的命题,并加以证明;
类似的命题,并加以证明;
(2)在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,利用上述(1)的结论求线段
的中点,利用上述(1)的结论求线段![]() 的长度;
的长度;
(3)在所有棱长均为![]() 平行六面体
平行六面体![]() 中,
中,![]() (
(![]() 为锐角定值),
为锐角定值),![]() 、
、![]() 分
分![]() 、
、![]() 所成的比为
所成的比为![]() ,求
,求![]() 的长度.(用
的长度.(用![]() ,
,![]() ,
,![]() 表示)
表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国际篮联篮球世界杯,将于2019年在北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传世界杯,某大学从全校学生中随机抽取了120名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:

(1)根据上表说明,能否有![]() 的把握认为收看篮球世界杯赛事与性别有关?
的把握认为收看篮球世界杯赛事与性别有关?
(2)现从参与问卷调查的120名学生中,采用按性别分层抽样的方法选取6人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
(i)求男、女学生各选取多少人;
(ii)若从这6人中随机选取3人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到2名男生的概率.
附: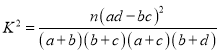 ,其中
,其中![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在极坐标系中,![]() 为极点,点
为极点,点![]() ,点
,点![]() .
.
(1)以极点为坐标原点,极轴为![]() 轴的正半轴建立平面直角坐标系,求经过
轴的正半轴建立平面直角坐标系,求经过![]() ,
,![]() ,
,![]() 三点的圆
三点的圆![]() 的直角坐标方程;
的直角坐标方程;
(2)在(1)的条件下,圆![]() 的极坐标方程为
的极坐标方程为![]() ,若圆
,若圆![]() 与圆
与圆![]() 相切,求实数
相切,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 的参数方程为
的参数方程为![]() (t为参数),以原点为极点,
(t为参数),以原点为极点,![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,曲线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,曲线![]() 关于
关于![]() 对称.
对称.
(1)求![]() 极坐标方程,
极坐标方程,![]() 直角坐标方程;
直角坐标方程;
(2)将![]() 向左平移4个单位长度,按照
向左平移4个单位长度,按照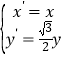 变换得到
变换得到![]() 与两坐标轴交于
与两坐标轴交于![]() 两点,
两点,![]() 为
为![]() 上任一点,求
上任一点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com