
【题目】已知函数![]() 的图象与
的图象与![]() 轴相切,且切点在
轴相切,且切点在![]() 轴的正半轴上.
轴的正半轴上.
(1)求曲线![]() 与
与![]() 轴,直线
轴,直线![]() 及
及![]() 轴围成图形的面积
轴围成图形的面积![]() ;
;
(2)若函数![]() 在
在![]() 上的极小值不大于
上的极小值不大于![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据导数的几何意义可得到![]() 得
得![]() ,
, ![]() ,解得
,解得![]() .(2)先求导
.(2)先求导![]() ,研究导函数的正负,当
,研究导函数的正负,当![]() 时,
时, ![]() 无极值;当
无极值;当![]() ,即
,即![]() 时,分析导数的正负使得极值
时,分析导数的正负使得极值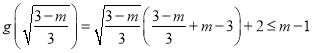 ,解出不等式即可。
,解出不等式即可。
解:(1)![]() ,
, ![]() 得
得![]() ,
,
由题意可得![]() ,解得
,解得![]() .
.
故![]() ,
, 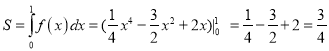 .
.
(2)![]() ,
, ![]()
当![]() 时,
时, ![]() 无极值;
无极值;
当![]() ,即
,即![]() 时,令
时,令![]() 得
得![]() ;
;
令![]() 得
得![]() 或.
或. ![]()
![]() 在
在![]() 处取得极小值,
处取得极小值,
当![]() ,即
,即![]() ,
, ![]() 在(-3,2)上无极小值,
在(-3,2)上无极小值,
故当![]() 时,
时, ![]() 在(-3,2)上有极小值
在(-3,2)上有极小值
且极小值为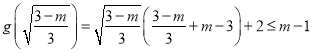 ,
,
即![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
又![]() ,故
,故![]() .
.
点睛:这个题目考查的是利用导数研究函数的极值;求导后出现二次函数形式,一般的讨论方法有:先看二次项系数是否为0,然后看能否因式分解,能分解的话,直接比较两根的大小,不能分解就由判别式和图像结合判断导函数的正负。


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中, ![]() 是抛物线
是抛物线![]() 的焦点,
的焦点, ![]() 是抛物线
是抛物线![]() 上的任意一点,当
上的任意一点,当![]() 位于第一象限内时,
位于第一象限内时, ![]() 外接圆的圆心到抛物线
外接圆的圆心到抛物线![]() 准线的距离为
准线的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,且
两点,且![]() ,点
,点![]() 为
为![]() 轴上一点,且
轴上一点,且![]() ,求点
,求点![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() ,其中
,其中![]() 为参数,
为参数, ![]() ,再以坐标原点
,再以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() ,
, ![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)已知点![]() ,且
,且![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,M是正方体ABCD﹣A1B1C1D1的棱DD1的中点,给出下列命题
①过M点有且只有一条直线与直线AB、B1C1都相交;
②过M点有且只有一条直线与直线AB、B1C1都垂直;
③过M点有且只有一个平面与直线AB、B1C1都相交;
④过M点有且只有一个平面与直线AB、B1C1都平行.
其中真命题是( )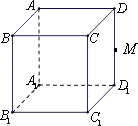
A.②③④
B.①③④
C.①②④
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC= ![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点. 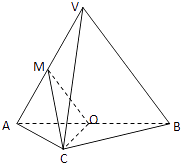
(1)求证:VB∥平面MOC.
(2)求证:平面MOC⊥平面VAB.
(3)求二面角C﹣VB﹣A的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=sin(x+1) ![]() ﹣
﹣ ![]() cos(x+1)
cos(x+1) ![]() ,则f(1)+f(2)+f(3)+…+f(2011)=( )
,则f(1)+f(2)+f(3)+…+f(2011)=( )
A.2 ![]()
B.![]()
C.﹣ ![]()
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自然数按如图的规律排列:则上起第2007行左起2008列的数为( ) 
A.20072
B.20082
C.2006×2007
D.2007×2008
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com