
【题目】某个部件由三个元件按如图所示的方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】为了了解某校学生喜欢吃零食是否与性别有关,随机对此校100人进行调查,得到如下的列表:已知在全部100人中随机抽取1人,抽到不喜欢吃零食的学生的概率为![]() .
.
喜欢吃零食 | 不喜欢吃零食辣 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 | 100 |
(Ⅰ)请将上面的列表补充完整;
(Ⅱ)是否有99.9%以上的把握认为喜欢吃零食与性别有关?说明理由.
下面的临界值表供参考:![]() ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|2x-1|-|x+1|.
(1)将f(x)的解析式写成分段函数的形式,并作出其图象;
(2)若a+b=1,对a,b∈(0,+∞),![]() +
+![]() ≥3f(x)恒成立,求x的取值范围.
≥3f(x)恒成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某火锅店为了了解气温对营业额的影响,随机记录了该店1月份其中5天的日营业额y(单位:万元)与该地当日最低气温x(单位:℃)的数据,如下表:
![]()
(1)求y关于x的线性回归方程![]() =
=![]() x+
x+![]() ;
;
(2)判断y与x之间是正相关还是负相关,若该地1月份某天的最低气温为6 ℃,用所求回归方程预测该店当日的营业额;
(3)设该地1月份的日最低气温X~N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2,求P(3.8<X≤13.4).
,σ2近似为样本方差s2,求P(3.8<X≤13.4).
附:①回归方程![]() 中,
中,![]() =
=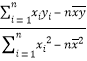 ,
,![]() =
=![]() ﹣
﹣![]() .
.
②![]() ≈3.2,
≈3.2,![]() ≈1.8.若X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.682 7,P(μ-2σ<X≤μ+2σ)=0.954 5.
≈1.8.若X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.682 7,P(μ-2σ<X≤μ+2σ)=0.954 5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的上顶点为
的上顶点为![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,点
,点![]() ,直线
,直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() (
(![]() 与
与![]() 不重合),过
不重合),过![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,是否存在定点
,是否存在定点![]() ,使
,使![]() 为定值?若存在求出
为定值?若存在求出![]() 的坐标,不存在说明理由?
的坐标,不存在说明理由?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在航天员进行的一项太空实验中,要先后实施6个程序,其中程序![]() 只能出现在第一步或最后一步,程序
只能出现在第一步或最后一步,程序![]() 实施时必须相邻,请问实验顺序的编排方法共有 ( )
实施时必须相邻,请问实验顺序的编排方法共有 ( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为平行四边形,PA⊥底面ABCD,
中,底面ABCD为平行四边形,PA⊥底面ABCD,![]() ,
,![]() ,
,![]() ,
,![]() .
.
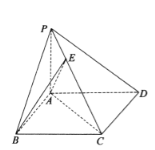
(1)求证:平面PCA⊥平面PCD;
(2)设E为侧棱PC上的一点,若直线BE与底面ABCD所成的角为45°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() . 已知过点
. 已知过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值.若存在,求出点
为定值.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com