
【题目】如图,已知抛物线![]() :
:![]() ,过直线
,过直线![]() 上一点
上一点![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,且点
两点,且点![]() 为
为![]() 中点、作直线
中点、作直线![]() 交
交![]() 轴于点
轴于点![]() .
.
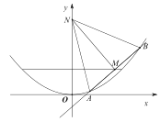
(1)求点![]() 的坐标;
的坐标;
(2)求![]() 面积的最大值.
面积的最大值.
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】如图,在极坐标系![]() 中,
中,![]() ,
,![]() ,弧
,弧![]() ,
,![]() ,
,![]() 所在圆的圆心分别为
所在圆的圆心分别为![]() ,
,![]() ,
,![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() .
.
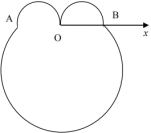
(1)写出曲线![]() ,
,![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 由
由![]() ,
,![]() ,
,![]() 构成,若曲线
构成,若曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() ),写出曲线
),写出曲线![]() 与曲线
与曲线![]() 的所有公共点(除极点外)的极坐标.
的所有公共点(除极点外)的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全民健身旨在全面提高国民体质和健康水平,倡导全民做到每天参加一次以上的健身活动,学会两种以上健身方法,每年进行一次体质测定.为响应全民健身号召,某单位在职工体测后就某项健康指数(百分制)随机抽取了30名职工的体测数据作为样本进行调查,具体数据如茎叶图所示,其中有1名女职工的健康指数的数据模糊不清(用x表示),已知这30名职工的健康指数的平均数为76.2.
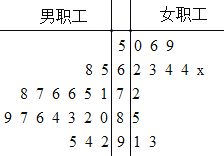
(1)根据茎叶图,求样本中男职工健康指数的众数和中位数;
(2)根据茎叶图,按男女用分层抽样从这30名职工中随机抽取5人,再从抽取的5人中随机抽取2人,求抽取的2人都是男职工的概率;
(3)经计算,样本中男职工健康指数的平均数为81,女职工现有数据(即剔除x)健康指数的平均数为69,方差为190,求样本中所有女职工的健康指数的平均数和方差(结果精确到0.1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() (M>0,
(M>0,![]() >0,0<
>0,0<![]() <
<![]() )的最小值是﹣2,最小正周期是2
)的最小值是﹣2,最小正周期是2![]() ,且图象经过点N(
,且图象经过点N(![]() ,1).
,1).
(1)求![]() 的解析式;
的解析式;
(2)在△ABC中,若![]() ,
,![]() ,求cosC的值.
,求cosC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月25日-27日,北京召开第二届“一带一路”国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,若对任意
,若对任意![]() ,都有
,都有![]() 成立,则称数列
成立,则称数列![]() 为“差增数列”.
为“差增数列”.
(1)试判断数列![]() 是否为“差增数列”,并说明理由;
是否为“差增数列”,并说明理由;
(2)若数列![]() 为“差增数列”,且
为“差增数列”,且![]() ,
,![]() ,对于给定的正整数m,当
,对于给定的正整数m,当![]() ,项数k的最大值为20时,求m的所有可能取值的集合;
,项数k的最大值为20时,求m的所有可能取值的集合;
(3)若数列![]() 为“差增数列”,
为“差增数列”,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com