
【题目】已知正△ABC边长为3,点M,N分别是AB,AC边上的点,AN=BM=1,如图1所示.将△AMN沿MN折起到△PMN的位置,使线段PC长为![]() ,连接PB,如图2所示.
,连接PB,如图2所示.
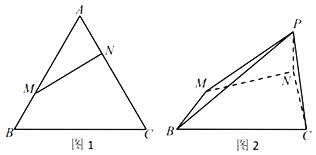
(Ⅰ)求证:平面PMN⊥平面BCNM;
(Ⅱ)若点D在线段BC上,且BD=2DC,求二面角M﹣PD﹣C的余弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】
(Ⅰ)推导出AN⊥MN,即PN⊥MN,PN⊥NC,从而PN⊥平面BCNM,由此能证明平面PMN⊥平面BCNM.
(Ⅱ)以N为坐标原点,NM为x轴,NC为y轴,NP为z轴,建立空间直角坐标系,利用向量法能求出二面角M﹣PD﹣C的余弦值.
解:(Ⅰ)证明:依题意,在△AMN中,AM=2,AN=1,∠A![]() ,
,
由余弦定理,![]() ,解得
,解得![]() ,
,
根据勾股定理得MN2+AN2=AM2,∴AN⊥MN,即PN⊥MN,
在图2△PNC中,PN=1,NC=2,PC![]() ,
,
∴PC2=PN2+NC2,∴PN⊥NC,
∵MN∩NC=N,∴PN⊥平面BCNM,
∵PN平面PMN,∴平面PMN⊥平面BCNM.
(Ⅱ)解:以N为坐标原点,NM为x轴,NC为y轴,NP为z轴,
建立空间直角坐标系,
则P(0,0,1),M(![]() ,0,0),D(
,0,0),D(![]() ,
,![]() ,0),C(0,2,0),
,0),C(0,2,0),
∴![]() (
(![]() ,0,﹣1),
,0,﹣1),![]() (
(![]() ,
,![]() ,0),
,0),
![]() (0,2,﹣1),
(0,2,﹣1),![]() (
(![]() ,
,![]() ,0),
,0),
设平面MPD的一个法向量![]() (x,y,z),
(x,y,z),
则 ,取y=1,得
,取y=1,得![]() (
(![]() ,1,3),
,1,3),
设平面PDC的法向量![]() (a,b,c),
(a,b,c),
则 ,取a=1,得
,取a=1,得![]() (1,
(1,![]() ,2
,2![]() ),
),
设二面角M﹣PD﹣C的平面角为θ,由图知θ是钝角,
∴cosθ .
.
二面角M﹣PD﹣C的余弦值为![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】天上有些恒星的亮度是会变化的,其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化.第一颗被描述的经典造父变星是在1784年.
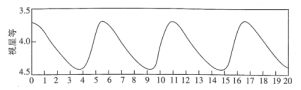
上图为一造父变星的亮度随时间的周期变化图,其中视星等的数值越小,亮度越高,则此变星亮度变化的周期、最亮时视星等,分别约是( )
A.5.5,3.7B.5.4,4.4C.6.5,3.7D.5.5,4.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知椭圆E经过点![]() ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点![]() ,
,![]() 在x轴上,离心率e
在x轴上,离心率e![]() .直线l是
.直线l是![]() 的平分线,则椭圆E的方程是_____,l所在的直线方程是_____.
的平分线,则椭圆E的方程是_____,l所在的直线方程是_____.
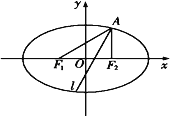
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个不透明的盒子中装有4个大小、形状、手感完全相同的小球,分别标有数字1,2,3,4.现每次有放回地从中任意取出一个小球,直到标有偶数的球都取到过就停止.小明用随机模拟的方法估计恰好在第4次停止摸球的概率,利用计算机软件产生随机数,每1组中有4个数字,分别表示每次摸球的结果,经随机模拟产生了以下21组随机数:由此可以估计恰好在第4次停止摸球的概率为( )
1314 1234 2333 1224 3322 1413 3124 4321 2341 2413 1224 2143 4312
2412 1413 4331 2234 4422 3241 4331 4234
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 只有一个公共点,点
只有一个公共点,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(1)求抛物线![]() 的方程;
的方程;
(2)①若![]() ,求证:直线
,求证:直线![]() 过定点;
过定点;
②若![]() 是抛物线
是抛物线![]() 上与原点不重合的定点,且
上与原点不重合的定点,且![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校高三大理班周三上午四节、下午三节有六门科目可供安排,其中语文和数学各自都必须上两节而且两节连上,而英语、物理、化学、生物最多上一节,则不同的功课安排有________种情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将曲线方程![]() ,先向左平移2个单位,再向上平移2个单位,得到曲线C.
,先向左平移2个单位,再向上平移2个单位,得到曲线C.
(1)点M(x,y)为曲线C上任意一点,写出曲线C的参数方程,并求出![]() 的最大值;
的最大值;
(2)设直线l的参数方程为![]() ,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com