
【题目】直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积达到最大时,
的面积达到最大时,![]() ________.
________.
【答案】![]()
【解析】
由圆的方程找出圆心![]() 坐标和半径
坐标和半径![]() ,同时把直线的方程整理为一般式方程,然后利用点到直线的距离公式表示出圆心
,同时把直线的方程整理为一般式方程,然后利用点到直线的距离公式表示出圆心![]() 到直线的距离
到直线的距离![]() ,即为圆
,即为圆![]() 中弦
中弦![]() 的弦心距,根据垂径定理得到垂足为弦
的弦心距,根据垂径定理得到垂足为弦![]() 的中点,由圆的半径,弦心距及弦的一半构成的直角三角形,利用勾股定理表示出弦
的中点,由圆的半径,弦心距及弦的一半构成的直角三角形,利用勾股定理表示出弦![]() 的长度,然后利用三角形的面积公式底乘以高除
的长度,然后利用三角形的面积公式底乘以高除![]() ,用含有
,用含有![]() 的式子表示出三角形
的式子表示出三角形![]() 的面积,并利用基本不等式
的面积,并利用基本不等式![]() 求出面积的最大值,以及面积取得最大值时
求出面积的最大值,以及面积取得最大值时![]() 的值,从而列出关于
的值,从而列出关于![]() 的方程,求出方程的解即可得到面积最大时
的方程,求出方程的解即可得到面积最大时![]() 的值.
的值.
解:由圆![]() ,
,
得到圆心坐标为![]() ,半径
,半径![]() ,
,
把直线的方程为![]() ,
,
整理为一般式方程得:![]() ,
,
.圆心![]() 到直线
到直线![]() 的距离
的距离![]()
弦![]() 的长度
的长度![]() ,
,
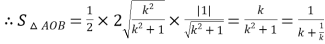 ,
,
又因为![]() ,
,![]()
当且仅当![]() 时取等号,
时取等号,![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.
解得![]()
故答案为:![]()


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
: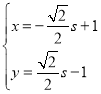 (
(![]() 为参数),以O为极点,
为参数),以O为极点,![]() 轴的非负半轴为极轴的极坐标系中,已知曲线
轴的非负半轴为极轴的极坐标系中,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,记曲线
,记曲线![]() 与
与![]() 的交点为
的交点为![]() .
.
(1)求点![]() 的极坐标;
的极坐标;
(2)设曲线![]() 与
与![]() 相交于A,B两点,求
相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个商场同时出售一款西门子冰箱,其中甲商场位于老城区中心,乙商场位于高新区.为了调查购买者的年龄与购买冰箱的商场选择是否具有相关性,研究人员随机抽取了1000名购买此款冰箱的用户作调研,所得结果如表所示:
50岁以上 | 50岁以下 | |
选择甲商场 | 400 | 250 |
选择乙商场 | 100 | 250 |
(1)判断是否有![]() 的把握认为购买者的年龄与购买冰箱的商场选择具有相关性;
的把握认为购买者的年龄与购买冰箱的商场选择具有相关性;
(2)由于乙商场的销售情况未达到预期标准,商场决定给冰箱的购买者开展返利活动具体方案如下:当天卖出的前60台(含60台)冰箱,每台商家返利200元,卖出60台以上,超出60台的部分,每台返利50元.现将返利活动开展后15天内商场冰箱的销售情况统计如图所示:与此同时,老张得知甲商场也在开展返利活动,其日返利额的平均值为11000元,若老张将选择返利较高的商场购买冰箱,请问老张应当去哪个商场购买冰箱

附: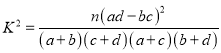 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的一个动点,且
上的一个动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交圆
交圆![]() :
:![]() 于另一点
于另一点![]() .若
.若![]() 的面积为3,求直线
的面积为3,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请120名同学每人随机写下一个x,y都小于1的正实数对
的值:先请120名同学每人随机写下一个x,y都小于1的正实数对![]() ,再统计其中x,y能与1构成钝角三角形三边的数对
,再统计其中x,y能与1构成钝角三角形三边的数对![]() 的个数m,最后根据统计个数m估计
的个数m,最后根据统计个数m估计![]() 的值.如果统计结果是
的值.如果统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有极值,且导函数
有极值,且导函数![]() 的极值点是
的极值点是![]() 的零点,给出命题:①
的零点,给出命题:①![]() ;②若
;②若![]() ,则存在
,则存在![]() ,使得
,使得![]() ;③
;③![]() 与
与![]() 所有极值之和一定小于0;④若
所有极值之和一定小于0;④若![]() ,且
,且![]() 是曲线
是曲线![]() 的一条切线,则
的一条切线,则![]() 的取值范围是
的取值范围是![]() .则以上命题正确序号是_____________.
.则以上命题正确序号是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知A,B分别为椭圆C:![]() (a>b>0)的左右顶点,P为椭圆C上异于A,B的任意一点,O为坐标原点,
(a>b>0)的左右顶点,P为椭圆C上异于A,B的任意一点,O为坐标原点,![]()
![]() =﹣4,△PAB的面积的最大值为
=﹣4,△PAB的面积的最大值为![]() .
.
(1)求椭圆C的方程;
(2)若椭圆C上存在两点M,N,分别满足OM∥PA,ON∥PB,求|OM||ON|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com