
【题目】设![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() 数列
数列![]() 的通项公式为
的通项公式为![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)将数列![]() ,
,![]() 中的公共项按从小到大的顺序构成数列
中的公共项按从小到大的顺序构成数列![]() ,请直接写出数列
,请直接写出数列![]() 的通项公式;
的通项公式;
(3)记![]() ,是否存在正整数
,是否存在正整数![]()
![]() ,使得
,使得![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在正整数m=11,n=1;m=2,n=3;m=6,n=11使得b2,bm,bn成等差数列
(3)存在正整数m=11,n=1;m=2,n=3;m=6,n=11使得b2,bm,bn成等差数列
【解析】试题分析:(1)利用基本元的思想,将已知条件转化为![]() 的形式,解方程组求得
的形式,解方程组求得![]()
![]() 的值,并求得
的值,并求得![]() 的通项公式.(2)由于
的通项公式.(2)由于![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,且
的等差数列,且![]() ,而
,而![]() 是,首项为
是,首项为![]() ,第二项为
,第二项为![]() 的等差数列,故
的等差数列,故![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,故通项公式为
的等差数列,故通项公式为![]() .(3)
.(3) ![]() ,先假设存在这样的数
,先假设存在这样的数![]() ,利用
,利用![]() 成等差数列,化简得到
成等差数列,化简得到![]() ,利用列举法求得
,利用列举法求得![]() 的值.
的值.
试题解析:
(1)设公差为![]() ,则
,则![]() ,由性质得
,由性质得![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() ,又由
,又由![]() 得
得![]() ,解得
,解得![]() ,
,
![]() 所以
所以![]() 的通项公式为
的通项公式为![]()
(2) ![]()
(3),假设存在正整数m、n,使得d5,dm,dn成等差数列,则d5+dn=2dm. ![]()
所以![]() +
+![]() =
=![]() , 化简得:2m=13-
, 化简得:2m=13-![]() .
.
当n-2=-1,即n=1时,m=11,符合题意;
当n-2=1,即n=3时,m=2,符合题意
当n-2=3,即n=5时,m=5(舍去) ;
当n-2=9,即n=11时,m=6,符合题意.
所以存在正整数m=11,n=1;m=2,n=3;m=6,n=11
使得b2,bm,bn成等差数列.


科目:高中数学 来源: 题型:
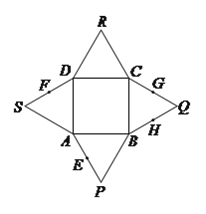
【题目】如图,已知四边形![]() 是正方形,
是正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 都是等边三角形,
都是等边三角形, ![]() 、
、![]() 、
、![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 、
、![]() 、
、![]() 的中点,分别以
的中点,分别以![]() 、
、![]() 、
、![]() 、
、![]() 为折痕将四个等边三角形折起,使得
为折痕将四个等边三角形折起,使得![]() 、
、![]() 、
、![]() 、
、![]() 四点重合于一点
四点重合于一点![]() ,得到一个四棱锥.对于下面四个结论:
,得到一个四棱锥.对于下面四个结论:
①![]() 与
与![]() 为异面直线; ②直线
为异面直线; ②直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]()
③![]() 平面
平面![]() ; ④平面
; ④平面![]() 平面
平面![]() ;
;
其中正确结论的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() 数列
数列![]() 的通项公式为
的通项公式为![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)将数列![]() ,
,![]() 中的公共项按从小到大的顺序构成数列
中的公共项按从小到大的顺序构成数列![]() ,请直接写出数列
,请直接写出数列![]() 的通项公式;
的通项公式;
(3)记![]() ,是否存在正整数
,是否存在正整数![]()
![]() ,使得
,使得![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半圆![]() 的直径为
的直径为![]() ,
, ![]() 为直径延长线上的一点,
为直径延长线上的一点, ![]() ,
, ![]() 为半圆上任意一点,以
为半圆上任意一点,以![]() 为一边作等边三角形
为一边作等边三角形![]() ,设
,设![]()
![]() .
.
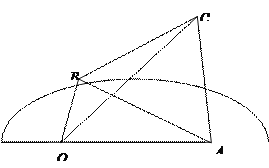
(1)当![]() 为何值时,四边形
为何值时,四边形![]() 面积最大,最大值为多少;
面积最大,最大值为多少;
(2)当![]() 为何值时,
为何值时, ![]() 长最大,最大值为多少.
长最大,最大值为多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图、正视图、侧视图、俯视图如图,M,N分别为A1B,B1C1的中点.


下列结论中正确的个数有 ( )
①直线MN与A1C相交.
②MN⊥BC.
③MN∥平面ACC1A1.
④三棱锥N-A1BC的体积为![]() =
=![]() a3.
a3.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点(
=1(a>b>0)过点( ![]() ,1),且以椭圆短轴的两个端点和一个焦点为顶点的三角形是等腰直角三角形.
,1),且以椭圆短轴的两个端点和一个焦点为顶点的三角形是等腰直角三角形.
(1)求椭圆的标准方程;
(2)设M(x,y)是椭圆C上的动点,P(p,0)是x轴上的定点,求|MP|的最小值及取最小值时点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量m ![]() (sin
(sin ![]() ,1),
,1), ![]() =(1,
=(1, ![]() cos
cos ![]() ),函数f(x)=
),函数f(x)= ![]()
(1)求函数f(x)的最小正周期;
(2)若f(α﹣ ![]() )=
)= ![]() ,求f(2α+
,求f(2α+ ![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com