
【题目】设函数f(x)=|x﹣1|﹣|2x+1|的最大值为m.
(Ⅰ)作出函数f(x)的图象;
(Ⅱ)若a2+2c2+3b2=m,求ab+2bc的最大值.
【答案】解:(Ⅰ)函数f(x)=|x﹣1|﹣|2x+1|=  , 画出图象如图,
, 画出图象如图,
(Ⅱ)由(Ⅰ)知,当x=﹣ ![]() 时,函数f(x)取得最大值为m=
时,函数f(x)取得最大值为m= ![]() .
.
∵a2+2c2+3b2=m= ![]() =(a2+b2)+2(c2+b2)≥2ab+4bc,
=(a2+b2)+2(c2+b2)≥2ab+4bc,
∴ab+2bc≤ ![]() ,当且仅当a=b=c=1时,取等号,
,当且仅当a=b=c=1时,取等号,
故ab+2bc的最大值为 ![]() .
.
【解析】(Ⅰ)利用分段函数,化简函数的解析式,从而作函数的图象,结合图象,求得函数的最大值m.(Ⅱ)由题意可得a2+2c2+3b2=m= ![]() =(a2+b2)+2(c2+b2),利用基本不等式求它的最值.
=(a2+b2)+2(c2+b2),利用基本不等式求它的最值.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1+2a2+…+nan=4﹣ ![]() .
.
(1)求数列{an}的通项公式;
(2)若bn=(3n﹣2)an , 求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , a1=1,an≠0,2anan+1=tSn﹣2,其中t为常数. (Ⅰ)设bn=an+1+an , 求证:{bn}为等差数列;
(Ⅱ)若t=4,求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() ),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
A.[ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣DEF中,侧面ABED是边长为2的菱形,且∠ABE= ![]() ,BC=
,BC= ![]() ,四棱锥F﹣ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM=
,四棱锥F﹣ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM= ![]() CF.
CF.
(Ⅰ)证明:直线GM∥平面DEF;
(Ⅱ)求二面角M﹣AB﹣F的余弦值.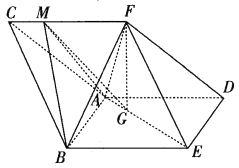
查看答案和解析>>
科目:高中数学 来源: 题型:
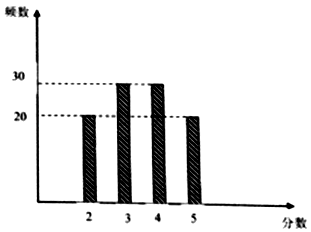
【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.
(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;
(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).
(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).
服务质量评分X | X≤5 | 6≤X≤8 | X≥9 |
等级 | 不好 | 较好 | 优良 |
奖惩标准(元) | ﹣1000 | 2000 | 3000 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要测量电视塔AB的高度,在C点测得塔顶的仰角是45°,在D点测得塔顶的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度是( )
A.30m
B.40m
C.![]() m
m
D.![]() m
m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数,﹣π<α<0),曲线C2的参数方程为
(α为参数,﹣π<α<0),曲线C2的参数方程为  (t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1的极坐标方程和曲线C2的普通方程;
(2)射线θ=﹣ ![]() 与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,AC⊥AB,AB=2AA1 , M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
(Ⅰ)若DE∥平面A1MC1 , 求 ![]() ;
;
(Ⅱ)求直线BG和平面A1MC1所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com